Вариант 9

Решение:

а) $\begin{array}{l}\cos3x=\cos(2x+x)=\cos2x\cos x-\sin2x\sin x=\\=(\cos^2x-\sin^2x)\cos x-2\sin^2\cos x=\\=(2\cos^2x-1)\cos x-2\cos x(1-\cos^2x)=4\cos^3-3\cos x\end{array}$

Тогда исходное уравнение равносильно уравнению

$\begin{array}{l}4\cos^3-3\cos x=-2\cos x\\\cos x(4\cos^2x-1)=0\\\cos x=0;\;\;x=\frac{\mathrm\pi}2+\mathrm{πn},\;\mathrm n\in\mathbb{Z}\\\mathrm{cosx}=\pm\frac12;\;\mathrm x=\pm\frac{\mathrm\pi}3+\mathrm{πk},\;\mathrm k\in\mathbb{Z}\end{array}$

б) С помощью числовой окружности отберем корни, принадлежащие указанному промежутку:

Ответ: а) $\frac{\mathrm\pi}2+\mathrm{πn},\;\mathrm n\in\mathbb{Z};$

$\pm\frac{\mathrm\pi}3+\mathrm{πk},\;\mathrm k\in\mathbb{Z};$

б) $-\frac{4\mathrm\pi}3,\;-\frac{2\mathrm\pi}3,\;-\frac{\mathrm\pi}2,\;-\frac{\mathrm\pi}3$

Решение:

а) В треугольнике $ABC\;AH\perp BC$, через точку $K$ проводим $KM\parallel AH$, отсюда $KM\perp BC$

$С_1С\perp(ABC)$, как высота прямой призмы, тогда $С_1С\perp KM$, поскольку $KM$ лежит в плоскости $(ABC)$, $KM\perp(BB_1C_1)$ по признаку перпендикулярности прямой и плоскости. Следовательно по признаку перпендикулярности плоскостей следует, что $(C_1MK)\perp(BB_1C_1)$, так как $(C_1MK)$ содержит прямую $KM$. Значит $(KC_1M)$ - искомое сечение.

б) Проекция $C_1K$ на плоскость $BB_1C_1C$: $MK\perp BC,\;C_1M$ - проекция $C_1K$. $\angle KC_1M$ - искомый угол.

$\cos\angle KC_1M=\frac{C_1M^2+C_1K^2-MK^2}{2C_1M\times C_1K}$

$\begin{array}{l}С_1M=\sqrt{C_1C^2+MC^2}=\sqrt{6+1}=\sqrt7\\C_1K=\sqrt{CC_1^2+CK^2}=\sqrt{6+4}=\sqrt{10}\\MK=KC\times\sin60^\circ=2\times\frac{\sqrt3}2=\sqrt3\end{array}$

$\cos\angle KC_1M=\frac{7+10-3}{2\times\sqrt{70}}=\frac{14}{2\sqrt{70}}=\frac{\sqrt{70}}{10}$

Ответ: $\frac{\sqrt{70}}{10}$

решим первое неравенство системы.

1. $\left(\frac14\right)^\frac{10-x^2}2\geq8^x;\;\;\;\;2^{x^2-10}\geq2^{3x};\;\;\;x^2-10\geq3x;$

$\begin{array}{l}\;\;x^2-3x-10\geq0;\;(x+2)(x-5)\geq0;\\x\in(-\infty;-2\rbrack\cup\lbrack5;+\infty)\end{array}$

2. Решим второе неравенство системы

$\log_{2x+5}(x^2-28x-7)>0$

ОДЗ $\left\{\begin{array}{l}\begin{array}{c}x^2-28x-7>0;\\2x+5>0;\end{array}\\\;\;\;\;\;\;2x+5\neq1;\end{array}\right.\left\{\begin{array}{l}\begin{array}{c}x>14+\sqrt{203}\;или\;x<14-\sqrt{203}\\x>-2,5\end{array}\\\;\;\;\;\;\;x\neq-2\end{array}\right.$

$\begin{array}{l}x\in(-2,5-2)\cup(-2;14-\sqrt{203})\cup(14+\sqrt{203};+\infty)\\(2x+5-1)(x^2-28x-7-1)>0\\(x+2)(x^2-28x-8)>0\\(x+2)(x-(14-2\sqrt{51}))(x-(14+2\sqrt{51}))>0\end{array}$

Учитывая множество решений первого неравенства, получим, что $x\in(14+2\sqrt{51};+\infty)$

Ответ $(14+2\sqrt{51};+\infty)$

Решение:

а) Пусть точки $O$ и $E$ расположены по одну сторону от прямой $BC$ (см. рисунок), то есть $\angle B+\angle C=180^\circ$, тогда $BE$ и $CE$ являются биссектрисами внутренних углов при вершинах $B$ и $C$ соответственно треугольника $BCO$. По свойству биссектрисы $BE$ точка $E$ равноудалена от сторон $BO$ и $BC$. Аналогично по свойству биссектрисы $CE$ точка $E$ равноудалена от сторон $BC$ и $OC$. Следовательно, точка $E$ равноудалена от всех сторон треугольника $BCO$ и является центром окружности, вписанной в этот треугольник.

Рассмотрим другой случай. Пусть точки $O$ и $E$ расположены по разные стороны от прямой $BC$(см. рисунок ниже), то есть $\angle B+\angle C>180^\circ$, тогда $BE$ и $CE$ являются биссектрисами внешних углов при вершинах $B$ и $C$ cсоответственно треугольника $BCO$. По свойству биссектрисы $BE$ точка $E$ равноудалена от прямых $BO$ и $BC$. Аналогично точка $E$ равноудалена от прямых $BC$ и $OC$. Следовательно, точка $E$ равноудалена от стороны $BC$ и продолжений сторон $BO$ и $OC$ треугольника $BCO$ и является центром вневписанной окружности этого треугольника. $EG,EF,EH\;-\;$ радиусы этой окружности.

б) Сумма углов выпуклого пятиугольника равна $540^\circ$. По условию задачи $\angle A=37^\circ,$$\angle D=143^\circ,$$\angle A+\angle D=180^\circ$. Если $\angle B+\angle C=180^\circ,$, что противоречит условию выпуклости прямоугольника. Значит $\angle B+\angle C>180^\circ,$, поэтому: $\bigtriangleup AGE=\bigtriangleup DHE$ по катету и острому углу. Аналогично $\bigtriangleup EHC=\bigtriangleup EFC.\;$ Последовательно имеем:

$S_{ABE}+S_{CDE}=S_{AGE}+S_{GBE}+S_{CHE}-S_{DHE}=S_{GBE\;}+\;S_{CHE}=$$=S_{BFE}+S_{FCE}=S_{BCE}=13$

$S_{ABCDE}=S_{ABE}+S_{CDE}+S_{BCE}=13+13=26$

Ответ: 26

Решение:

Посчитаем площадь участка $S=9,5\times3,5km^2=3325$га.

Стоимость аренды трактора $600\times S$ рублей, стоимость солярки $32\times15\times S$ рублей. Обозначим оплату тракториста за обработку 1га за $x$ рублей. Тогда его зарплата будет составлять $S\times x$ рублей, а техническое обслуживание трактора 5% от $S\times x$. По условию $600S+32\times15S+Sx+0,05Sx\leq4009950$

$x\leq120$

За 1га наибольшая оплата тракториста 120 рублей, за норму 75га наибольшая оплата $75\times120=9000$ рублей.

Ответ: 9000 рублей.

Решение:

Сделаем замену $tgx+2=t$, тогда уравнение пример вид

$t^2-(3a^2+2a-4)t+(3a^2-5)(2a+1)=0.$

Пользуясь обратной теоремой Виета, запишем корни этого уравнения $t_1=2a+1,\;t_2=3a^2-5$, откуда:

$\left\{\begin{array}{l}tgx=2a-1,\\tgx=3a^2-7.\end{array}\right.$

Изобразим эскиз графика функции $y=tgx$ при $x\in\left[-\frac{\mathrm\pi}2;\mathrm\pi\right]$ (см. рисунок). Очевидно, что при $x\in\left[-\frac{\mathrm\pi}2;\mathrm\pi\right]$ уравнение $tgx=b$ имеет 2 решения при $b\leq0$ и 1 решение при $b>0$.

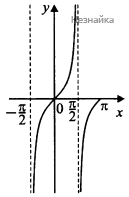
Значит, исходное уравнение на отрезке $x\in\left[-\frac{\mathrm\pi}2;\mathrm\pi\right]$ имеет ровно 2 решения в одном из двух случаев:

$\begin{array}{l}1)\;2a-1=3a^2-7\leq0\\2)\;\left\{\begin{array}{l}\begin{array}{c}2a-1>0\\3a^2-7>0\end{array}\\2a-1\neq3a^2-7.\end{array}\right.\end{array}$

Рассмотрим каждый из этих случаев отдельно.

Решив вспомогательное уравнение $3a^2-7=2a-1$ получим $a=\frac{1\pm\sqrt{19}}3$. При $a=\frac{1+\sqrt{19}}3$ имеет место неравенство $2a-1=-\frac13+\frac{2\sqrt{19}}3>0$, а при $a=\frac{1-\sqrt{19}}3$, соответственно,$2a-1=-\frac13-\frac{2\sqrt{19}}3<0$.

Значит, $a=\frac{1-\sqrt{19}}3$ соответствует условию задачи.

Решим систему неравенств:

$\left\{\begin{array}{c}2a-1>0\\3a^2-7>0\\2a-1\neq3a^2-7\end{array}\right.\;\;\left\{\begin{array}{c}a>\frac12\\a<-\sqrt{\frac73}\;или\;a>\sqrt{\frac73}\\a\neq\frac{1\pm\sqrt{19}}3\end{array}\right.$

Так как $\frac{1+\sqrt{19}}3>\sqrt{\frac73}$, то

значит ответ будет: $\left\{\frac{1-\sqrt{19}}3\right\}\cup\left(\sqrt{\frac73};\;\frac{1+\sqrt{19}}3\right)\cup\left(\frac{1+\sqrt{19}}3;\;+\infty\right)$