Вариант 5
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
В равнобедренном треугольнике ABC с основанием AC=6√5 проведена высота BH=6 см. Найдите радиус описанной окружности треугольника ABC (в см).
Шар вписан в цилиндр. Площадь поверхности шара равна 18. Чему равна площадь полной поверхности цилиндра
В магазин поступила партия телевизоров в количестве 25 шт. Известно, что у пяти из них отсутствует в комплекте дистанционное управление. Найдите вероятность того, что Володя приобретёт полностью укомплектованный телевизор.
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна . Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна . Вероятность того, что система по ошибке забракует исправную батарейку, равна.
Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
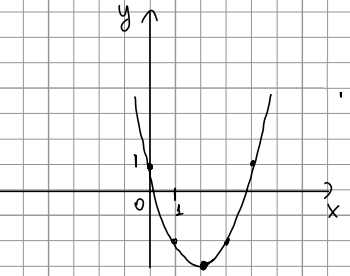
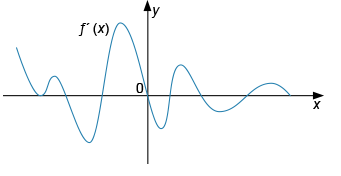
На рисунке изображен график производной функции f′ (x). Определите количество точек максимума функции.
Для расчета сложных процентов по вкладу с учётом внутригодового начисления используется формула: F=P(1+rm)nm, где P — исходная сумма (в руб.), r — годовая процентная ставка (r=%100), n — количество лет, m — количество внутригодовых начислений.
В конце первого года на счету было 165 375 руб. Определите исходную сумму вклада (в руб.), если процентная ставка 10 % и внутригодовых начислений было 2.
Некоторое количество раствора уксусной кислоты разбавили тремя литрами воды и получили 20 %-ный раствор. Определите начальную концентрацию раствора (в %), если, добавив в него 2 л 25 %-ного раствора, получили концентрацию в 40 %.
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите наибольшее значение функции f(x)=sin(x−13π12)−cos(x−13π12) на отрезке [π3;11π12]
Найдем производную и определим точки максимума на отрезке [π3;11π12]
f′(x)=cos(x−13π12)+sin(x−13π12)
f′(x)=0
tg(x−13π12)=−1
x−13π12=3π4+πn
x=116π+πn — на интервале [π3;11π12] только один экстремум при n=-1: x=56π.
При x56π — возрастает, значит x=56π — точка минимума.
Найдем наибольшее значения функции на границах интервала
f(1112π)=sin(11π12−13π12)−cos(11π12−13π12)=0,5−√32<0
f(π3)=sin(π3−13π12)−cos(π3−13π12)=0 — искомое наибольшее значение функции
Дано уравнение 21+tg2x=1+sinx.
А) Решите уравнение.
Б) Найдите его корни, принадлежащие отрезку [−7π2;−2π].
А) Преобразуем левую часть уравнения и получим:
21cos2x=1+sinx
2cos2x=1+sinx
2(1−sin2x)−1−sinx=0
2sin2x+sinx−1=0
Пусть sinx=t. Тогда
2t2+t−1=0
t1=−1 t2=12
Обратная замена:
sinx=−1 x=−π2+2πn, n∈Z - посторонний, т.к. по ОДЗ cosx≠0
sinx=12; x1=π6+2πn , x2=5π6+2πn, n∈Z
Б) Нанесем корни на числовую прямую и определим, какие корни входят в отрезок
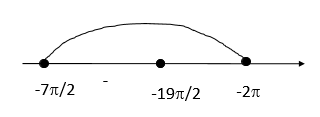
Ответ: А) π6+2πn,5π6+2πn,n∈Z
Б) −19π6
PH - высота правильной четырехугольной пирамиды РАВСD, О - точка пересечения медиан треугольника ВСР.
А) Докажите, что прямые РН и АО не имеют общих точек.
Б) Найдите угол между прямыми РН и АО, если известно, что АВ=РН.
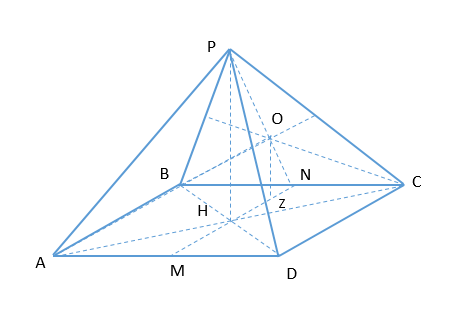
А) Опустим из O перпендикуляр на (ABC) OZ⊥(ABC)
⇒(AOZ)⊥(ABC), PH⊥(ABC)⇒PH∥(AOZ)
т.к PH∉(AOZ), AO∈(AOZ), то PH и AO не имеют общих точек, ч.т.д.
Б) ∠(PH;AO)=∠AOZ
Пусть AB=PH=a
Рассмотрим △HPN и △ZON, △HPN∼△ZON (по двум углам: ∠H=90∘;∠Z=90∘;∠PNZ - общий)
⇒NONP=NZNH=OZPH, NOOP=12 (по свойству медиан треугольника) ⇒NONP=13 (т.к. NP=NO+OP)
⇒OZ=13PH=13a
ZN=13HN;HN=12DC=12a (как средние линии △DBC, HN∥DC;BN=NC
⇒ZN=16a;MZ=56a
Из △AMZ по теореме Пифагора: AZ=√MZ2+AM2=√25a236+a24=a√25+936=a√346
∠AOZ=arctg(AZOZ)=arctg(a√346⋅3a)=arctg(√342)
Ответ: arctg√342
Решите неравенство log(x−2)2(9x−3)≤0.
ОДЗ: x−2≠−1;x−2≠1;x−2≠0;32x−3>0
x≠1;3;2 x>12
Преобразуем неравенство:
12logx−2(32x−3)≤0
ln(32x−3)ln(x−2)≤0
Нули числителя: ln(32x−3)=0
32x−3=1
2x=log34
x=log32
Нули знаменателя: x−2=1 x=3
Нанесем на числовую прямую и расставим знаки:
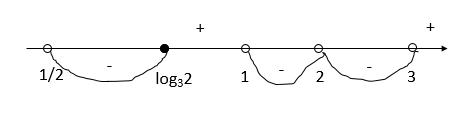
Ответ: (0,5; log32]⋃(1; 2)⋃(2; 3)
1 декабря 2016 года Валерий взял в банке в кредит 523 тыс. руб. под 10% годовых сроком на три года. Схема выплаты кредита следующая: 30 ноября каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем с 1-го до 30-го декабря Валерий выплачивает банку часть долга. По договоренности с банком было определено, что второй платеж будет в три раза меньше первого, а третий - в два раза меньше второго. Сколько рублей должен будет выплатить банку Валерий в декабре 2018 года?
Решение: покажем в таблице кредитную историю Валерия:

Решим получившееся уравнение:
696113−10,46x=0
x=69611310.46=66550, 2x=133100
Ответ: 133100
На гипотенузе АВ прямоугольного треугольника АВС как на стороне построен квадрат вне треугольника.
А) Докажите, что прямая, соединяющая центр квадрата и центр вписанной в треугольник АВС окружности, проходит через точку С.
Б) Найдите расстояние между центром квадрата и центром вписанной в треугольник АВС окружности, если известно, что АС= 4√2, BC= 3√2.
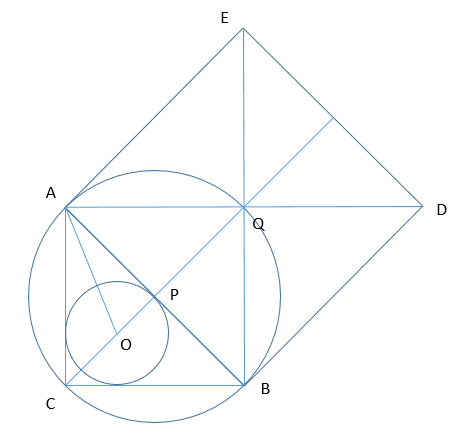
А) Если доказать, что CQ - биссектриса ∠ACB, то будет доказано, что C∈OQ, т.к. CO - биссектриса ∠ACB (по свойству касательных, проведенных из одной точки)
Рассмотрим четырехугольник CAQB:
∠C+∠Q=180∘,∠A+∠B=∠QAB+∠QBA+∠BAC+∠ABC=180∘⇒CAQB может быть вписан в окружность
⇒∠QBA=∠QCA=45∘,∠QAB=∠QCB=45∘⇒(т.к. опираются на равные дуги) CQ - биссектриса ∠ACB⇒C∈OQ, ч.т.д.
Б) AC=4√2, BC=3√2 , OQ - ?
△CPB∼△APQ (по двум углам):∠PCB=∠PAQ=45∘, ∠CPB=∠APQ как вертикальные ⇒∠PBC=∠PQA
Пусть ∠CAB=x, тогда ∠ABC=90∘−x=∠PQA, ∠QAO=45∘+x2 (т.к. ∠PAO=∠CAO по свойству касательных)
Тогда для △AOQ: ∠OQA+∠QAO+∠AOQ=180∘
90∘−x+45∘+x2+∠AOQ=180∘⇒∠AOQ=45∘+x2
∠AOQ=∠QAO⇒△AQO - равнобедренный, AQ=OQ=5
Ответ: 5
Найдите все значения параметра а, при каждом из которых система уравнений
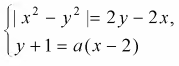
имеет ровно одно решение.
Решение: используем графический способ решения системы. Сначала построим график для первого уравнения.
1 сл: x2−y2>0
x2=y2|x|=|y|
График функции имеет вид "креста" (ветви креста - биссектрисы прямых углов) , слева и справа между "ветвями креста"- решение неравенства
Имеем уравнение:x2−y2=2y−2x
(x+1)2−(y+1)2=0
|x+1|=|y+1|
График функции есть крест, ветви которого- биссектрисы прямых углов. График смещен на (-1;-1)
2 сл: x2−y2<0
x2=y2|x|=|y|
График функции имеет вид "креста" (ветви креста - биссектрисы прямых углов), сверху и снизу между "ветвями креста"- решение неравенства
Имеем уравнение:−x2+y2=2y−2x
(x−1)2−(y−1)2=0
|x−1|=|y−1|
График функции есть крест, ветви которого- биссектрисы прямых углов. График смещен на (1;1)
3 сл: x2−y2=0
Значит 0=2y−2x
y=x
Построим график и семейство прямых, отражающие возможные решения системы уравнений. Для этого проанализируем уравнение прямой: график прямой всегда проходит через точку (2;-1)

Имеем решение:
(-∞; -2] — прямая будет пересекать график в одной точке (в нижней части плоскости).
a= -1 — прямая пересекает y=x, и не пересекает две другие прямые с угловым коэффициентом -1, они параллельны.
[0; +∞) — прямая будет пересекать график в одной точке (в верхней части плоскости), но исключается значение а = 1, т.к. тогда прямая параллельна y=x
Ответ: (-∞; -2]⋃{-1}⋃[0; 1)⋃(1; +∞)
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||