Вариант 3

Найдем первую производную и определим точки экстремума:

f'(x)=10x⁵+2x⁴-35x²-7x

Найдем точки, в которых f'(x)=0

10x⁵+2x⁴-35x²-7x=0

2x⁴(5x+1)-7x(5x+1)=0

x(2x³-7)(5x+1)=0

x₁=0

2x³-7=0

x³=7/2 —> $x_2=\sqrt[3]{\\frac72}>1$

5x+1=0

x₃=-1/5

Функция при x<-1/5 убывает, так как производная отрицательная. При -1/5<x<0 — функция возрастает, производная — положительная. При 0<x<$\sqrt[3]{\\frac72}$ — функция убывает, производная — отрицательная. При x>$\sqrt[3]{\\frac72}$ — функция возрастает, производная — положительная.

Точка максимума на промежутке $\left[-1;1\right]$: х=0

А) Преобразуем левую и правую части:

$3^\frac{2sin^2x}{cosx}\cdot3^\frac{3sinx}{cosx}=3^\frac{-1}{cosx}$

$3^\frac{2sin^2x+3sinx+1}{cosx}=3^0$

Основания равны, значит и показатели при этих основаниях тоже равны. Получим:

$2sin^2x+3sinx+1=0$

Осуществим замену. Пусть t=sinx

$2t^2+3t+1=0$

$t_1=-1$$t_2=-\frac12$

Обратная замена:

$sinx=-1$

$x=-\frac\pi2+2\pi n$

$sinx=-\frac12$

$x=(-1)^{k+1}\frac\pi6+\pi k$, $k\in Z$

Б) Нанесем на числовую прямую наши корни:

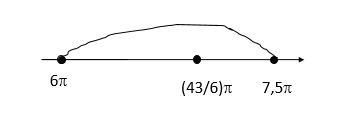
В отрезок вошел только один корень $\frac{43\pi}6$

Ответ: А) $\left(-1\right)^{k+1}\cdot\frac\pi6+\pi k,\;k\in Z$

Б) $\frac{43\pi}6$

Решение:

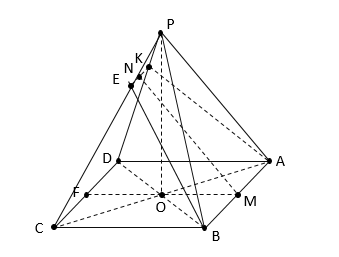
А) Плоскость $\alpha$ пересекает грань $CPD$ по прямой $EK\parallel AB$. т.к. пирамида правильна, то $EB=KA$, т.е. сечение $AKEB$ – равнобедренная трапеция.

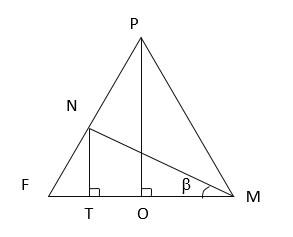
$\angle NMF$ – линейный угол двугранного угла $CABN$, т.к. $\alpha\cap(ABC)=AB$.

$FM\perp AB$, $M$ – середина $AB$

$NM\perp AB$ (высота трапеции)

$O$ – середина $FM$,т.е $FO=OM=10$

Из $\bigtriangleup FPO$ : $tg\angle F=\frac{PO}{OF}=\frac{45}{4\cdot10}=\frac98$

Пусть $FT=x$, тогда $TM=20-x$

Из $\bigtriangleup FNT$ : $NT=FT\;tg\angle F=\frac98x$

Из $\bigtriangleup TNM$ : $NT=TM\;tg\beta=(20-x)\cdot\frac34$

$\frac98x=(20-x)\cdot\frac34$

$x=8$

$FN=8$, $NT=9$

$ER=NT=9$

$\bigtriangleup COP\sim\bigtriangleup CER$, $\frac{CE}{CP}=\frac{ER}{PO}=\frac9{\frac{45}4}=\frac45$$\Rightarrow CE:EP=4:1$ или $EP:EC=1:4$

Б) Из $\bigtriangleup NTM$: $NT$=9,$TM=12$, $NM^2=9^2+12^2=81+144=225$,$NM=15$

$\bigtriangleup PEK\sim\bigtriangleup PCD$

$\frac{PE}{PC}=\frac{EK}{CD}=\frac15\Rightarrow EK=\frac15CD=\frac15\cdot20=4$

$S_{трап}=\frac{AB+EK}2\cdot NM=\frac{20+4}{20}\cdot15=12\ast15=180$

Ответ: 180

Решение:

$\frac{2^{3x}-6\cdot2^{2x}+12\cdot2^x-2^3}{4(2^x-3)}\geq\frac{2^{3x}-4\cdot2^{2x}+2\cdot2^x}{(3-2^x)(3+2^x)}$

$\frac{(2^x-2)^3(3+2^x)+4\cdot2^x(2^x-2)^2}{4(2^x-3)(2^x+3)}\geq0$

$\frac{(2^x-2)^2((2^x-2)(3+2^x)+4\cdot2^x)}{4(2^x-3)(2^x+3)}\geq0$

$\frac{(2^x-2)^2(2^x+5\cdot2^x-6)}{4(2^x-3)(2^x+3)}\geq0$

$2^x=2$

Нули числителя: x=1 – корень кратности 2

$2^{2x}+5\cdot2^x-6=0$

$2^x=1$

$x=0$

$2^x=-6$. Корней нет, так как -6<0

Нули знаменателя: $x=log_23$

Решим на числовой прямой:

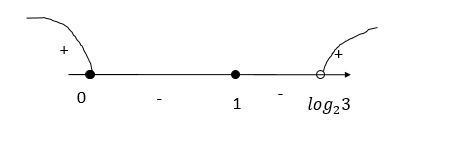
Ответ: (-∞; 0]⋃{1}⋃(log23; +∞)

Решение: найдем время,потраченное вторым автомобилем до первой встречи из пункта В: $t=\frac{48}{80}$=0.6

Вычислим скорость второго автомобиля: $v_2=\frac{120-48}{0.6}=120$

Получим, что первый на весь путь АВ потратил $t_1=\frac{48}{80}=6$ , а второй -$t_2=\frac{48}{120}=4$

Время, за которое проехал второй до места второй встречи с первым: $\frac{48}{120}=0,4$ часа $=24$ мин

Время, которое второй потратил до второй встречи равно 4 часа + 20 мин + 24 мин = 4 часа 44 мин, а первого- 6 часов – 0,6 = 5,4 часа = 5 часов 24 мин

Найдем время, на которое второй выехал позже: 5 часов 24 – 4 часа 44 мин=40 мин

Найдем время, которое потратил второй до места первой встречи: $\frac{3200}{\frac{60}{120-80}}=\frac86$ (час)

В итоге получим расстояние от А до места первой встречи $\frac{120\cdot8}6=160$км

Ответ:160 км

Решение:

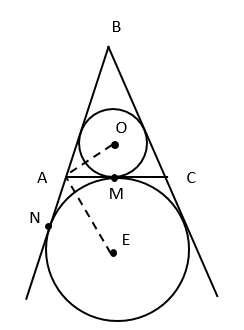
А) $AO$ – биссектриса $\angle BAM$ ( по свойству касательных , проведенных из одной точки)

$AE$ – биссектриса $\angle MAN$

$\angle BAM+\angle MAN=180^\circ$, $2\angle OAM+2\angle MAE=180^\circ$

$\angle OAM+\angle MAE=90^\circ$, т.е. $\bigtriangleup OAE$ – прямоугольный

$AM\perp OM$, т.к. $BM$ – высота,медиана равнобедренного треугольника $\bigtriangleup АВС$

$М$ – середина $АС$

Вторая окружность, также касается $АС$ в точке $М$

$АМ$ – высота $\bigtriangleup АОЕ$, проведенная из прямого угла, значит $АМ=\sqrt{МО\cdot МЕ}$

$АМ=\frac12АС$,$МО=\frac12d_1$, $МE=\frac12d_2$, тогда $\frac12АС=\sqrt{\frac12d_1\cdot\frac12d_1}=\frac12\sqrt{d_1\cdot d_2}$

Б) Пусть $\angle ОАМ=\alpha$, тогда $\angle ВАМ=2\alpha$

Пусть $МЕ=x$, $AM=y$

Из $\bigtriangleup ABM$: $tg2\alpha=\frac{BM}{AM}=\frac8y$

Из $\bigtriangleup OAM$:$tg\alpha=\frac{OM}{AM}=\frac3y$

$tg2\alpha=\frac{2tg\alpha}{1-tg^2\alpha}$

$\frac8y=\frac{2\cdot\frac3y}{1-\frac9{y^2}}$

$\frac8y=\frac{6y}{y^2-9}$

$8(y^2-9)=6y^2$

$8y^2-6y^2=8\cdot9$

$y=6$

$AM=6$

$AM=\sqrt{OM\cdot ME}$

$6=\sqrt{3x}$

$ME=x=12$

Ответ:12

Решение: преобразуем функцию

$f(x)=x^2(3x^2-8ax+6(a^2-1))$ ветви вверх

Возьмем производную:

$f'(x)=12x^3-24ax^2+12(a^2-1)x$

$f'(x)=0$

x=0

$x^2-2ax+(a^2-1)=0$

$D=a^2-(a^2-1)=1$$x_1=a+1$,$x_2=a-1$

1 сл: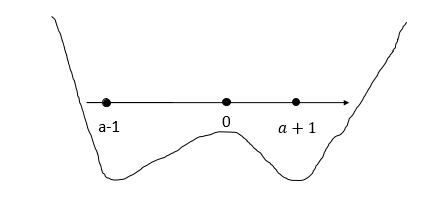

a-1 0.т.е. при $-1<a<1$ x=0-экстремум

2 сл: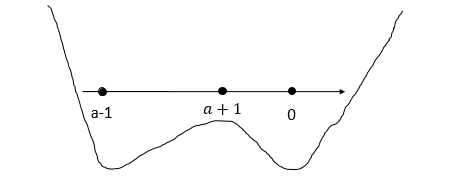

a-1<0 и a+1<0.т.е. при а < -1 x_max = a+1

3 сл: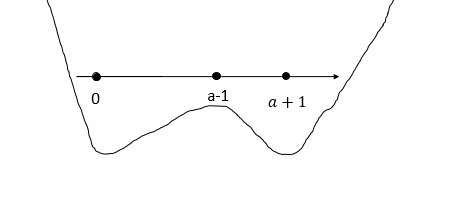

a-1>0 и a+1>0.т.е при $a>1$ x_max = a-1

4 сл: $a=\pm1$. тогда имеем корень х=0- корень кратности 2, корень х=2 или х=-2. Значит, имеем функцию, не имеющую максимум функции

Ответ: при а < -1 x_max = a+1, при $a>1$ x_max = a-1, при $-1<a<1$ x_max = 0.