Решение:

Сделаем замену $tgx+2=t$, тогда уравнение пример вид

$t^2-(3a^2+2a-4)t+(3a^2-5)(2a+1)=0.$

Пользуясь обратной теоремой Виета, запишем корни этого уравнения $t_1=2a+1,\;t_2=3a^2-5$, откуда:

$\left\{\begin{array}{l}tgx=2a-1,\\tgx=3a^2-7.\end{array}\right.$

Изобразим эскиз графика функции $y=tgx$ при $x\in\left[-\frac{\mathrm\pi}2;\mathrm\pi\right]$ (см. рисунок). Очевидно, что при $x\in\left[-\frac{\mathrm\pi}2;\mathrm\pi\right]$ уравнение $tgx=b$ имеет 2 решения при $b\leq0$ и 1 решение при $b>0$.

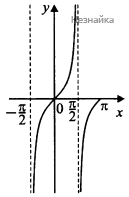
Значит, исходное уравнение на отрезке $x\in\left[-\frac{\mathrm\pi}2;\mathrm\pi\right]$ имеет ровно 2 решения в одном из двух случаев:

$\begin{array}{l}1)\;2a-1=3a^2-7\leq0\\2)\;\left\{\begin{array}{l}\begin{array}{c}2a-1>0\\3a^2-7>0\end{array}\\2a-1\neq3a^2-7.\end{array}\right.\end{array}$

Рассмотрим каждый из этих случаев отдельно.

Решив вспомогательное уравнение $3a^2-7=2a-1$ получим $a=\frac{1\pm\sqrt{19}}3$. При $a=\frac{1+\sqrt{19}}3$ имеет место неравенство $2a-1=-\frac13+\frac{2\sqrt{19}}3>0$, а при $a=\frac{1-\sqrt{19}}3$, соответственно,$2a-1=-\frac13-\frac{2\sqrt{19}}3<0$.

Значит, $a=\frac{1-\sqrt{19}}3$ соответствует условию задачи.

Решим систему неравенств:

$\left\{\begin{array}{c}2a-1>0\\3a^2-7>0\\2a-1\neq3a^2-7\end{array}\right.\;\;\left\{\begin{array}{c}a>\frac12\\a<-\sqrt{\frac73}\;или\;a>\sqrt{\frac73}\\a\neq\frac{1\pm\sqrt{19}}3\end{array}\right.$

Так как $\frac{1+\sqrt{19}}3>\sqrt{\frac73}$, то

значит ответ будет: $\left\{\frac{1-\sqrt{19}}3\right\}\cup\left(\sqrt{\frac73};\;\frac{1+\sqrt{19}}3\right)\cup\left(\frac{1+\sqrt{19}}3;\;+\infty\right)$