Задание № 8242
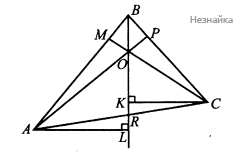
На сторонах АВ, ВС и АС треугольника АВС лежат точки М, Р и R соответственно, причём отрезки BR, СМ и АР пересекаются в точке О.
а) Докажите, что AMMB⋅BPPC⋅CRRA=1.
б) Найдите длину стороны АВ, если ВС = 10, АС = 13, ВМ : ВР = 3 : 2, CR = 9.
Решать другие задания по теме: Экономические задачи
Показать ответ
Комментарий:
 Ответ:
Ответ:
Решение:
Проведем из точек A и C перпендикуляры к прямой BR, тогда CK∥AL (см. рисунок )

△ARL∼△CRK, значит ALCK=ARRC
SAOBSCOB=0,5OB×AL0,5OB×CK=ARRC; SCOBSAOB=RCAR
Аналогично доказывается, что SAOCSBOC=AMMB и SBOASCOA=BPPC. Перемножим пропорции:
SCOBSAOB×SBOASCOA×SAOCSBOC=CRRA×AMMB×BPPC=1
б) AC=13;CR=6,5;AR=13−6,5=6,5; CRAR=1; BMBP=32;BM=1,5BP;; 1×AM1,5BP×BPPC=1; AM=1,5PC
AB=BM+AM=1,5BP+1,5PC=1,5(BP+PC)=1,5BC=15
Ответ: 15
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.