Решение:

а) Рассмотрим усеченную четырехугольную пирамиду $ABCDA_1B_1C_1D_1$, Описанную около шара (см. рисунок) Пусть $A_1B_1C_1D_1$ - квадрат со стороной а, $ABCD$ - квадрат со стороной b. По условию $S_{ABCD}=9S_{A_1B_1C_1D_1}$ , $b^2=9a^2$ следовательно $b=3a$.

Пусть $M$ - середина $AB$, $N$ - середина $CD$. Проведем прямую $MN$ сечение, перпендикулярное плоскости основания. Пусть $KP$ - отрезок, по которому плоскость сечения пересекается с верхним основанием, $KP\parallel MN$, $K$ - середина $A_1B_1$, $P$ - середина $C_1D_1$. Трапеция $KPMN$ описана около круга, образованного сечением шара рассматриваемой плоскостью. Тогда $KP+MN=MK+PN=4a$, $MK=PN=2a$. C другой стороны, $PN$ - высота трапеции $DD_1C_1C$ и $PN=2a=\frac{3a+a}2=\frac{CD+C_1D_1}2$, что и требовалось доказать.

б) Рассмотрим трапецию $MKPN$ (см. рисунок)

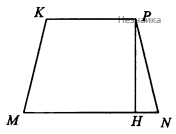
$MN\perp CD$, $PN\perp CD$, поэтому $\angle PNM$ - линейный угол искомого двугранного угла

$HN=\frac{MN-KP}2=\frac{3a-a}2=a$

$\cos\angle PNH=\frac{HN}{PN}=\frac a{2a}=\frac12$

$\angle PNH=\frac{\mathrm\pi}3$

Ответ: $\frac{\mathrm\pi}3$