Задание № 26407
Основания трапеции равны 4 и 12, одна из боковых сторон равна 12√3, а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
Решать другие задания по теме: Графики функций
Показать ответ
Комментарий:
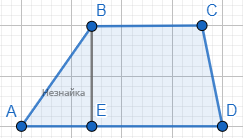
По условию BC=4, AD=12, AB=12√3 ∠ABC=120°.
Проведем высоту BE. Тогда угол ∠ABE=∠ABC-90°=120°-90°=30°
cos∠ABE=cos30°=√3/2=BE/AB
BE=AB•√3/2=12√3•√3/2=18
Площадь трапеции равна произведению полусуммы оснований и высоты
S=(BC+AD)•BE/2=(4+12)•18/2=144
Ответ: 144
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.