Вариант 3
Часть 1.
Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.
Прочитайте внимательно текст и выполните задания 1–5
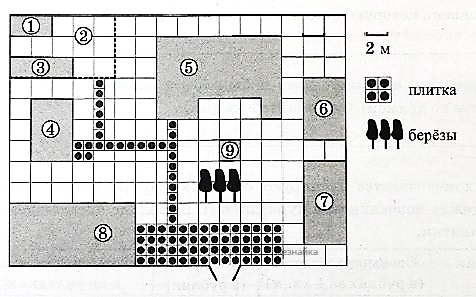
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.
Сопоставьте объекты, указанные в таблице, с цифрами, которыми эти объекты обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность из пяти цифр.
| Объекты | компостная яма | баня | теплица | пруд | жилой дом |
| Цифры |
Тротуарная плитка продаётся в упаковках по 6 штук. Сколько упаковок понадобилось купить владельцам домохозяйства для того, чтобы выложить все дорожки и площадку между коровником и курятником?
Найдите расстояние от жилого дома до теплицы (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.
Владельцы домохозяйства планируют обновить всю тротуарную плитку (и дорожки, и площадку между коровником и курятником). В таблице представлены условия трёх поставщиков плитки.
| Поставщик | Стоимость плитки (в руб. за 1 кв.м.) | Доставка (в руб.) | Работы по демонтажу старой плитки и по укладке новой (в руб.) |
| 1 | 300 | 5000 | 10000 |
| 2 | 300 | 6000 | 12250 |
| 3 | 320 | бесплатно | 6800 |
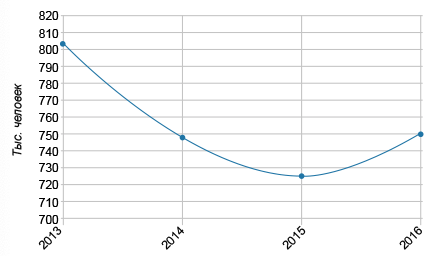
На графике указано количество учеников, сдававших ЕГЭ в определённый год. Определите, в каком году ЕГЭ сдавало наименьшее количество человек.
Маша покупает набор посуды стоимостью 2300 рублей. 14 % от покупки она оплачивает баллами с карты постоянного клиента (один балл равен одному рублю). Сколько баллов изначально было на карте, если Маша потратила на покупку только половину баллов?
Два человека вышли из одного дома. Первый поехал на велосипеде на север со скоростью 15 км/ч. Второй пошел пешком на запад со скоростью 8 км/ч. Какое расстояние (в км) будет между ними через 2 часа?
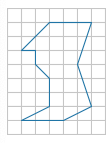
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь (в см2 ).
Основания трапеции равны 4 и 12, одна из боковых сторон равна 12√3, а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
Укажите номера верных утверждений. Выберите 2 варианта из списка.
1) Сумма углов параллелограмма, прилежащих к одной стороне, не превосходит 180°
2) Точка пересечения медиан треугольника является центром описанной вокруг этого треугольника окружности.
3) Длина средней линии трапеции равна сумме длин её оснований.
4) Через любые две точки проходит не более одной прямой.
В коробке с игрушками лежат 8 кубиков жёлтого цвета, 14 кубиков красного цвета и 10 кубиков синего цвета. Найдите вероятность того, что первый случайно вынутый кубик окажется жёлтого цвета.
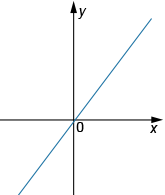
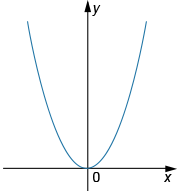
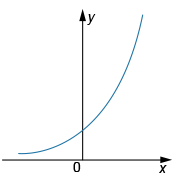
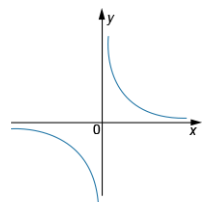
На каком рисунке изображена гипербола?
1) 
2) 
3) 
4) 
Выпишите цифры, которые соответствуют графикам.
Последовательность задана формулой dn=2n2−6. Какое из указанных чисел является членом этой последовательности?
1) 29
2) 3
3) 12
4) 4
Упростите выражение 12−4x4x2−24x+36 и найдите его значение при x = 4. В ответ запишите полученное число.
Часть 2.
При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Решите неравенство (x+2)2≥4(x+2)
(x+2)2≥4(x+2)
(x+2)2-4(x+2)≥0
x2+4x+4-4x-8≥0
x2-4≥0
x2≥4
x≤-2 или x≥2
Ответ: (-∞;-2], [2;∞)
Один мастер может выполнить задание на 15 дней быстрее, чем другой. После того, как первый мастер проработал 10 дней, его сменил другой и закончил работу за 30 дней. За сколько дней могут выполнить всю работу два мастера, работая одновременно?
Пусть Х дней надо одному мастеру для выполнения работы, а другому Х+15 дней. Работоспособность первого 1/Х, а второго - 1/(Х+15). После того, как первый проработал 10 дней было сделано 10/Х работы и, затем, еще 30/(Х+15) работы вторым за 30 дней. В результате работа была выполнена.
10x+30x+15=1
10x+150+30xx(x+15)=1
40x+150=x2+15x
x2−25x−150=0
x1=30 - дней надо одному мастеру для выполнения задания
x2=-5 - лишний корень
30+15=45 дней необходимо другому мастеру
Работоспособность обоих мастеров 1/30 + 1/45 = 1/18. Значит необходимо 18 часов для совместного выполнения задания.
Ответ: 18
Постройте график функции (x2+x)⋅|x|x+1 и определите, при каких значениях а прямая y = а не имеет с графиком ни одной общей точки.
Раскроем знак модуля:
при x<0
у=(x2+x)•(-x)/(x+1) - упростим выражение при x≠-1, так как при x=-1 - разрыв функции типа дырка.
у=-x2 - парабола, ветви вниз, без растяжений и сжатий.
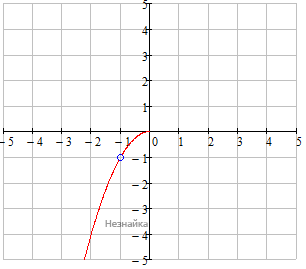
при x≥0
у=(x2+x)•x/(x+1)
у=x2 - парабола, ветви вверх, без растяжений и сжатий.
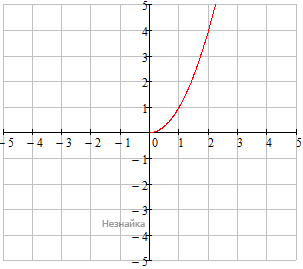
Объединяем полученные графики и получаем график функции (x2+x)⋅|x|x+1
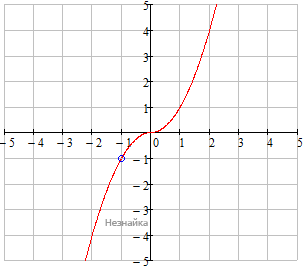
Прямая y = а не имеет с графиком ни одной общей точки, только в точке разрыва a=-1.
Ответ: -1
Через концы хорды, длина которой 30, проведены две касательные, до пересечения в точке А. Найдите расстояние от точки А до хорды, если радиус окружности равен 17.
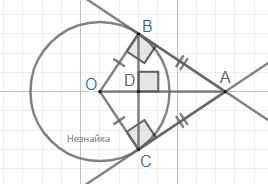
OB=OC=17 - радиусы, значит они перпендикулярны соответствующим касательным BA и CA. Прямоугольные треугольники ABO и ACO равны между собой по катету и общей гипотенузе, поэтому AB=AC, треугольник ABC - равнобедренный и AD - биссектриса ∠BAC. Таким образом, AD - еще и высота, и медиана равнобедренного треугольника, и искомое расстояние от точки А до хорды.
В прямоугольном △OBD : OB=17, BD=30/2=15. По теореме Пифагора OD=√(OB2-BD2)=8
По теореме о пропорциональных отрезках: BD2=OD•AD
AD=BD2/OD=152/8=28,125
Ответ: 28,125
В четырехугольнике две стороны параллельны, а диагонали взаимно перпендикулярны. Докажите, что если в данный четырехугольник можно вписать окружность, то две другие стороны четырёхугольника равны между собой.
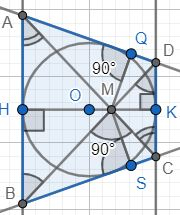
Так как стороны AB и DC параллельны, то углы ∠DBA=∠BDC и ∠BAC=∠DCA. Треугольники △MAB и △MDC прямоугольные, так как диагонали перпендикулярны, △MAB и △MDC - подобны по двум равным углам.
Значит MAMC=MBMD=ABCD=k
Для подобия прямоугольных треугольников △DMA и △CMA необходимо выполнения условия MDMC=MAMB - что противоречит соотношениям MAMC=MBMD=k.
Поэтому рассмотрим прямоугольные треугольники △DMA , △AMB , △BMC , △CMD
△DMA:
MQ=MA⋅MDAD - высота прямоугольного треугольника
MAMC=MBMD → MA⋅MD=MC⋅MB
MQ=MA⋅MDAD=MC⋅MBAD
△AMB:
MH=MB⋅MABC
MAMC=MBMD=ABCD → MB=AB⋅MDCD и MA=AB⋅MCCD
MH=MB⋅MABC=MD⋅MACD=MB⋅MCCD
△BMC:
MS=MC⋅MBBC
MAMC=MBMD → MA⋅MD=MC⋅MB
MS=MC⋅MBBC=MA⋅MDBC
△CMD:
MK=MC⋅MDCD
MAMC=MBMD=ABCD → MD=MB⋅CDAB и MC=MA⋅CDAB
MK=MC⋅MDCD=MA⋅MDAB=MC⋅MBAB
——————————————————————
MQ=MA⋅MDAD=MC⋅MBAD
MH=MB⋅MABC=MD⋅MACD=MB⋅MCCD
MS=MC⋅MBBC=MA⋅MDBC
MK=MC⋅MDCD=MA⋅MDAB=MC⋅MBAB
Почленным деление правых и левых частей выражений получаем следующие соотношения:
MHMS=BCCD
MKMQ=ADAB
MHMQ=ADCD
MKMS=BCAB
Так как окружность вписана в четырехугольник, то AB+CD=AD+BC :
MHMS=BCCD → CD=BCMSMH
MKMQ=ADAB → AB=ADMQMK
ADMQMK+BCMSMH=AD+BC → MQMK=1 и MSMH=1
MHMQ=ADCD → AD=CDMHMQ
MKMS=BCAB → BC=ABMKMS
AB+CD=CDMHMQ+ABMKMS → MHMQ=1 и MKMS=1
MQ=MK ; MS=MH ; MH=MQ ; MK=MS → MQ=MK=MS=MH=R - радиус окружности
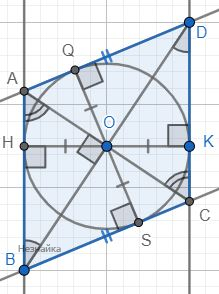
MHMK=k=1 → △DMA , △AMB , △BMC , △CMD равны между собой, а значит ABCD ромб и AD=BC.
В треугольнике АВС угол В равен 30°. Через точки А и В проведена окружность радиуса 2, касающаяся прямой АС в точке А. Через точки В и С проведена окружность радиуса 3, касающаяся прямой АС в точке С. Найдите длину стороны АС.
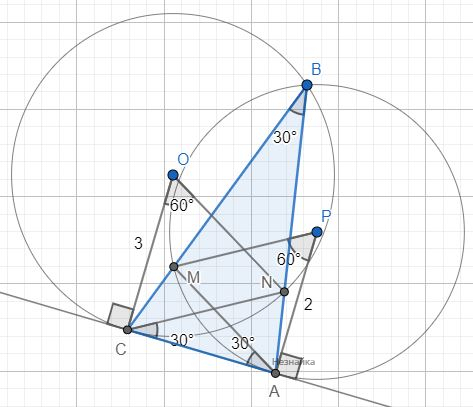
PA и OC - радиусы окружностей равные 2 и 3 соответственно и перпендикулярные касательной AC.
Вписанный угол MBA равен 30° и опирается на дугу ⌒МА, величина которой в два раза больше - 60°. Центральный угол ∠МРА опирается на ту же дугу, и так же равен 60°. Значит △МРА равносторонний, так как ∠МРА=60° и РА,РМ - радиусы, т.е. все углы в △МРА по 60°.
∠МАС=180°-90°-∠РАМ=180°-90°-60°=30°
Аналогично, дуга ⌒СN равна 60° и угол ∠МРА=60°, треугольник △NOC - равносторонний.
∠NCA=180°-90°-∠OCN=180°-90°-60°=30°
△ABC и △ACN: ∠ВАС - общий, ∠ABC=∠NCA=30° → △ABC~△ACN - подобны → ∠ACB=∠ANC
△ABC и △ACM: ∠ВСА - общий, ∠ABC=∠МАС=30° → △ABC~△ACM - подобны → ∠ACB=∠AMC
∠ACB=∠ANC=∠AMC и ∠NCA=∠МАС=30° → △ACN~△CAM - подобны → ACAM=CNAC
AC=√AM⋅CN=√РА⋅ОС=√2⋅3=√6
Ответ: √6
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||