Вариант 9
Часть 1.
Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.
Прочитайте внимательно текст и выполните задания 1–5
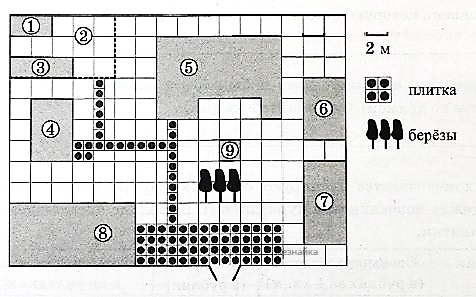
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.
Сопоставьте объекты, указанные в таблице, с цифрами, которыми эти объекты обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность из пяти цифр.
| Объекты | жилой дом | компостная яма | фонтан | баня | теплица |
| Цифры |
Тротуарная плитка продаётся в упаковках по 15 штук. Сколько упаковок понадобилось купить владельцам домохозяйства для того, чтобы выложить все дорожки и площадку между коровником и курятником?
Найдите расстояние от бани до теплицы (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.
Владельцы домохозяйства планируют обновить всю тротуарную плитку (и дорожки, и площадку между коровником и курятником). В таблице представлены условия трёх поставщиков плитки.
| Поставщик | Стоимость плитки (в руб. за 1 кв.м.) | Доставка (в руб.) | Работы по демонтажу старой плитки и по укладке новой (в руб.) |
| 1 | 500 | 3000 | 2500 |
| 2 | 500 | 4000 | бесплатно |
| 3 | 555 | бесплатно | 3500 |
На праздник были закуплены воздушные шары. Известно, что 3 из 50 шаров лопаются при надувании. Найдите вероятность того, что первый надутый шарик не лопнет.
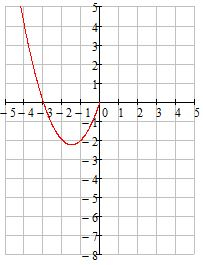
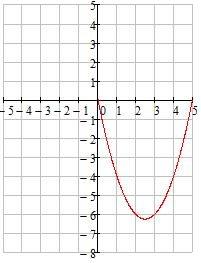
На рисунке изображен график квадратичной функции y=f(x). Определите какой из приведенных функций соответствует график.
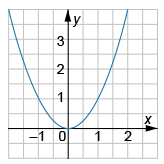 .
.
1) y=2x+1
2) y=x2
3) y=2x2
4) y=−2x2
Объём конуса можно вычислить по формуле V=13πr2h, где r — радиус основания конуса, h — высота конуса. Найдите радиус основания конуса (в м), объем которого равен 32π м высота — 6 м.
В равнобедренной трапеции ABCD меньшее основание BC равно 5 см, боковая сторона — 4 см, а угол при основании равен — 60∘. Найдите большее основание AD (в см).
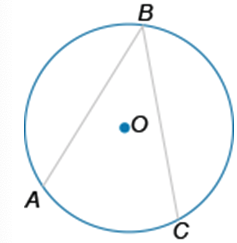
В окружности с центром в точке O проведены две хорды AB и BC. Дуга ABC равна 280∘. Найдите угол ABC (в градусах).
Найдите площадь равнобедренного треугольника (в см2) высота которого, проведенная к основанию, равна 8 см, а боковая сторона — 10 см.
Укажите 2 номера неверных утверждений.
1) Развёрнутый угол больше 180∘
2) В треугольнике может быть только один тупой угол.
3) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники равны.
4) В равнобедренном треугольнике высота, проведённая к основанию, является медианой.
Часть 2.
При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Решите систему уравнений 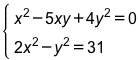
1) х2-5ху+4у2=0
х2-4ху-ху+4у2=0
х(х-4у)-у(х-4у)=0
(х-у)(х-4у)=0 → х-у=0 или х-4у=0
2){х−у=02х2−у2=31 или {х−4у=02х2−у2=31
3){х−у=02х2−у2=31
х=у
2х2-х2=21
х2=31
х1=√31 у1=√31
х2=-√31 у2=-√31
4){х−4у=02х2−у2=31
х=4у
2(4у)2-у2=31
32у2-у2=31
31у2=31
у2=1
у3=1 х3=4
у4=-1 х4=-4
Ответ: (-4;-1), (4;1), (-√31;-√31), (√31;√31)
В каждом вагоне находится одинаковое число пассажиров. Количество пассажиров в одном вагоне превосходит число вагонов на 9. Когда на станции во второй вагон вошли 10 человек, а из остальных вышло по 10 человек, то число пассажиров во втором вагоне оказалось равным числу пассажиров, оставшихся во всех остальных вагонах. Сколько пассажиров было первоначально в каждом вагоне?
Пусть Х людей былло первоначально в каждом вагоне, тогда вагонов было Х-9. Всего людей Х(Х-9).
Во второй вагон вошли 10 человек и людей в нем стало Х+10. В остальных вагонах людей Х(Х-10).
Из остальных вагонов вышло по 10 человек и стало (Х-10)(Х-10) человек.
Число пассажиров во втором вагоне оказалось равным числу пассажиров, оставшихся во всех остальных вагонах:
Х+10=(Х-10)(Х-10)
Х+10=Х2-20Х+100
Х2-21Х+90=0
D=212-4•1•90=81
Х1=(21-9)/2=6 - условию задачи не удовлетворяет
Х2=(21+9)/2=15
Ответ: 15
Постройте график функции y=x2−4|x|−x и определите, при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
у=х2-4|х|-х
Раскроем знак модуля
1) При х<0
у=х2-4(-х)-х
у=х2+3х
у=х2+3х=х2+3х+1,52-1,52=(х+1,5)-2,25 - парабола, ветви вверх, вершина (-1,5;-2,25)
2) При х≥0
у=х2-4х-х
у=х2-5х
у=х2-5х=х2-5х+2,52-2,52=(х-2,5)-6,25 - парабола, ветви вверх, вершина (2,5;-6,25)
3) Совмещаем оба графика и определяем при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
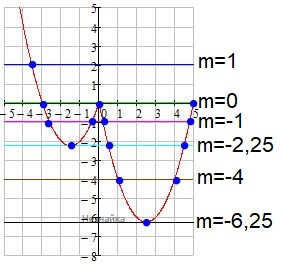
При mє(0;∞) прямая y=m и график функции имеют 2 общие точки
При m=0 и m=-2,25 прямая y=m и график функции имеют 3 общие точки
При mє(-6,25;-2,25) прямая y=m и график функции имеют 2 общие точки
При m=-6,25 прямая y=m и график функции имеют 1 общую точку
Ответ: [-6,25;-2,25], [0;∞)
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
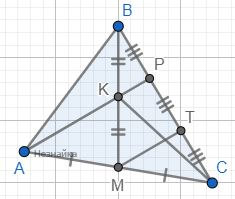
Проведём отрезок MT параллельный AP. Так как М это середина АС, то МТ средняя линия треуольника △APС, значит СТ=РТ. Аналогично КР средняя линия треугольника △ВМТ, следовательно ВР=РТ
Пусть площадь треугольника △ВКР равна S.
Рассмотрим треугольник △КРС: он имеет общую высоту с треугольником △ВКР и вдвое большее основание, тогда его площадь равна 2S. Площадь треугольника △ВКС равна 3S и такую же площадь имеет треугольник △МКС поскольку они имеют одну высоту, проведённую из вершины С и равные основания. Аналогично площадь треугольника △МКС равна площади треугольника △МКА, а площадь треугольника △МКА равна площади треугольника △ВКА.
Итого: S△ВКР=S ; S△КРС=2S ; S△ВКС=S△МКС=S△МКА=S△ВКА=3S
Таким образом:
S△АВС=S△ВКС+S△МКС+S△МКА+S△ВКА=12S
S△КРСМ=S△КРС+S△МКС=5S
S△АВС/S△КРСМ=12/5
Ответ: 12/5
На медиане KF треугольника MKP отмечена точка E. Докажите, что если EM=EP, то KM=KP.
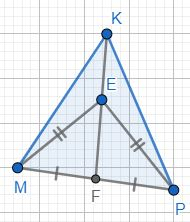
Треугольники △MEF=△PEF, так как EM=EP, FM=FP, EF - общая. Тогда ∠MEF=∠PEF, а в сумме они ∠MEF+∠PEF=180°, значит ∠MEF=∠PEF=90°.
Прямоугольные треугольники △MKF=△PKF, так KF - общая и FM=FP.
Следовательно KM=KP.
В прямоугольном треугольнике АВС точки D и E лежат соответственно на катетах BC и AC так, что CD = CE = 1. Точка M — точка пересечения отрезков AD и BE Площадь треугольника BMD больше площади треугольника AME на 1/2. Известно, что AD = √10. Найдите длину гипотенузы AB.
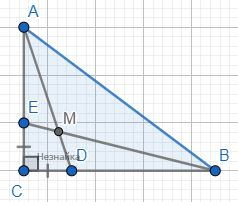
1) По теореме Пифагора △ACD:
AC2+CD2=AD2
AC2+12=√102
AC2=9
AC=3
2) S△BMD-S△AME=1/2
Добавим и вычтем SEMDC
S△BMD+SEMDC-S△AME-SEMDC=1/2
S△BEC=S△BMD+SEMDC=BC•CE/2=BC/2
S△ADC=S△AME+SEMDC=AC•CD/2=3/2
S△BEC-S△ADC=1/2
BC/2 - 3/2 = 1/2
BC-3=1
BC=4
3) По теореме Пифагора △ABC:
AB=√(AC2+BC2)=√(32+42)=5
Ответ: 5
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||