Вариант 10
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
AD — основание равнобедренной трапеции ABCD. Диагонали трапеции пересекаются под прямым углом в точке O, угол A равен 75 °. Найдите длину боковой стороны (в см), если OD = 6√3 см.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины равны 12 и 8. Объем параллелепипеда равен 672. Найдите 3 ребро, выходящее из той же вершины.
В состязании по математике в команде «Незнайка в твоих штанах» 12 человек, из них три девочки. Отвечающего на вопрос члены жюри выбирают случайным образом. Найдите вероятность того, что выбранный участник — мальчик.
На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 3 прыгуна из Голландии и 6 прыгунов из Аргентины. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что тринадцатым будет выступать прыгун из Аргентины.
Изменение координаты точки выражается функцией f(t)=252√t2+t22+6√t, где t (в с) — время движения. Определите, какова была мгновенная скорость (в м/с) при t = 9 c.
Для вычисления коэффициента эффективности миграции (в %) используется формула K=P−BP+B⋅100, где P — численность прибывших (в тыс. человек), B — численность выбывших (в тыс. человек). Сколько тысяч человек должно выехать из страны, чтобы коэффициент эффективности миграции достиг 10 % при 11 тыс. чел. прибывших?
Алексею необходимо выполнить грузоперевозку продукции массой 41,6 т. В первый день он перевез 200 кг товара. Найдите, на сколько тонн он ежедневно увеличивал массу привезённого товара по сравнению с предыдущим днём, если известно, что всю работу он выполнил за 13 дней.
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите точку минимума функции f(x)=2x−128xln2
Найдем производную:
f'(x)=2x•ln2-128•ln2
Теперь точки экстремума:
f'(x)=2x•ln2-128•ln2=0
2x=128
x=7 — точка минимума
Дано уравнение √−ctgx⋅(2cos2x−cosx−1)=0.
А) Решите уравнение.
Б) Укажите его корни из промежутка [15π2;9π].
А) ОДЗ: sinx≠0;ctgx<0
√−ctgx=0
cosx=0
x=π2+πn, n∈Z
2cos2x−cosx−1=0
a=2;b=−1;c=−1;a+b+c=0⇒x1=1;x2=ca
⇒cosx=1;cosx=−12
x=2πn - не соответствует ОДЗ, x=−2π3+2πk;x=2π3+2πk, k∈N
x=−2π3+2πk - не соответствует ОДЗ
Б) Нанесем на числовую прямую и определим, какие корни входят в промежуток:
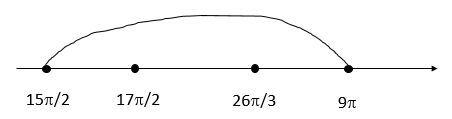
А) 2π3+2πn;π2+πk,n,k∈Z
Б) 15π2;17π2;26π3
Дана правильная треугольная призма ABCA1B1C1.
А) Докажите, что прямая В1С1 перпендикулярна линии пересечения плоскостей АВС1 и АСВ1.
Б) Найдите угол между плоскостями АВС1 и АСВ1, если известно, что АВ=2, АА1=2.
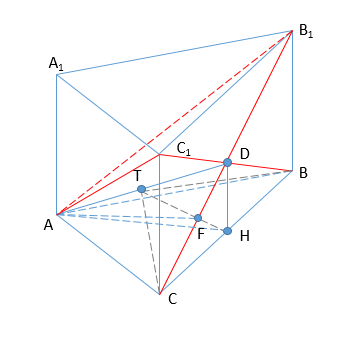
А) Доказать, что прямая В1С1 перпендикулярна линии пересечения плоскостей АВС1 и АСВ1.
т. A∈(ABC1). т. A∈(ACB1)
C1B∈(ABC1), B1C∈(ACB1)
C1B∩CB1=D⇒D∈(ABC1);D∈(ACB1)
и AD∈(ABC1);AD∈(ACB1)⇒AD - линия пересечения (ABC1) и (ACB1)
Имеем: необходимо доказать B1C1⊥AD
Опустим из D перпендикуляр DH на CB (DH⊥CB)
т.D - не только высота треугольника, но и медиана,т.е.CH=HB
т.к. △ABC - правильный, то AH - не только медиана, но и высота ⇒AH⊥CB
Тогда AD⊥CB (по теореме о трех перпендикулярах)
А т.к. CB∥C1B1, то AD⊥C1B1, что и требовалось доказать
Б) AB=2;AA1=2;∠((ABC1);(ACB1)−?
Опустим из C и B перпендикуляры на AD. Исходя из равенства △ADC=△ADB (по трем сторонам) они упадут на одну точку, пусть т.Т
Имеем CT⊥AD,BT⊥AD, ∠CTB - линейный угол искомого двугранного угла
△CTB - равносторонний ⇒TH⊥CB
Тогда sin(12∠CTB)=HCCT
Из △CHD по теореме Пифагора: CD=√CH2+HD2 (HD=12BB1) CD=√1+1=√2
Из △CHA по теореме Пифагора: AH=√AC2−CH2 AH=√4−1=√3
Из △AHD по теореме Пифагора: AD=√AH2+HD2 AH=√3+1=2
Имеем AC=AD⇒△CAD - равнобедренный . Опустим из А AF⊥CD
При этом CF=FD=12CD=√22
Тогда из △AFC по теореме Пифагора AF=√AC2−CF2=√4−12=√72
С одной стороны, S△ADC=12CT⋅AD, с другой стороныS△ADC=12AF⋅CD⇒CT⋅AD=AF⋅CD⇒2CT=√72⋅√2⇒CT=√72
sin(12∠CTB)=1√72=2√7⇒cos(12∠CTB)=√1−47=√37, sin(∠((ABC1);(ACB1)))=2⋅2√7⋅√37=4√37 и cos(∠((ABC1);(ACB1)))=√1−16⋅349=17
⇒∠((ABC1);(ACB1))=arccos(17)
Ответ: arccos17
Решите неравенство log2+x13+log2−x3≤0.
ОДЗ: 2+x>0⇒x>−2;2−x>0⇒x<2;2+x≠1;2−x≠1
log313log3(2+x)+log33log3(2−x)≤0
−1log3(2+x)+1log3(2−x)≤0
−log3(2−x)+log3(2+x)log3(2+x)⋅log3(2−x)≤0
Нули числителя: log32+x2−x=0
2+x2−x=1
2+x=2−x
x=0
Нули знаменателя: log3(2−x)=0⇒2−x=1⇒x=1
log3(2+x)=0⇒2+x=1⇒x=−1
Нанесем на числовую прямую нули числителя и знаменателя и расставим знаки:
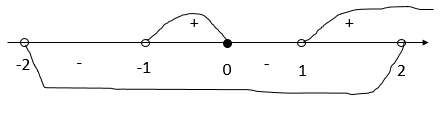
Ответ: (-1;0]⋃(1; 2)
В начале января 2017 года планируется взять кредит в банке на S млн. рублей, где S — целое число, на 4 года. Условия его возврата таковы:
- каждый июль долг возрастает на 10% по сравнению с началом текущего года;
- с августа по декабрь каждого года необходимо выплатить часть долга;
- в январе каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:
| Начало года | 2017 | 2018 | 2019 | 2020 | 2021 |
| Долг (в млн. рублей) | S | 0,7S | 0,4S | 0,2S | 0 |
Найдите наибольшее значение S, при котором разность между наибольшей и наименьшей выплатами не будет превышать 2 млн. руб.
Найдем выплаты за каждый год и составим таблицу
| Год | 2017 | 2018 | 2019 | 2020 |
| Выплаты (в млн. рублей) | 1,1S-0,7S=0,4S | 1,1*0,7S-0,4S=0,37S | 1,1*0,4S-0,2S=0,24S | 1,1*0,2S-0S=0,22S |
Найдем наибольшее значение S, при котором разность между наибольшей и наименьшей выплатами не будет превышать 2 млн. руб. Для этого определим, что наибольшая выплата сделана в 2017г., а наименьшая- в 2020г. Получим следующее неравенство:
0.4S−0.22S≤2
S≤11.11
Следовательно, т.к. по условию S - целое число, то наибольшее значение S=11
Ответ: 11
В неравнобедренном треугольнике АВС ∠BAC = 45°. Продолжение биссектрисы CD треугольника пересекает описанную около него окружность υ1 в точке Е. Окружность υ2, описанная около треугольника ADE, пересекает продолжение стороны АС в точке F.
А) Докажите, что DE — биссектриса угла FDB.
Б) Найдите радиус окружности υ2, если известно, что АС=6, AF=2.
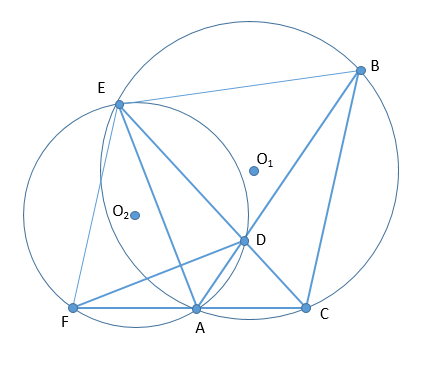
А) ∠CEB=∠BAC=45∘ (опираются на одну и ту же дугу)
∠ABE=∠ECA (опираются на одну и ту же дугу)
⇒∠EDB=180∘−∠CEB−∠ABE=180∘−45∘−∠ECA=135∘−∠ECA
∠ECB=∠ECA (из условия)
Тогда ∠EDB=∠ECB+∠CBD (как внешний) или∠EDB=∠ECA+∠CBD
∠AEC=∠CBD (опираются на одну и ту же дугу)
∠AFD=∠AED (опираются на одну и ту же дугу в окружности v2)⇒∠AFD=∠CBD
∠EDA=180∘−∠EDB (как смежные)
Найдем ∠FDE: ∠FDE=∠EDA−∠FDA;∠FDA=180∘−∠FAD−∠FDA (из △FAD), где ∠DFA=∠CBD (смотреть выше) и ∠FAD=180∘−∠DAC=180∘−45∘=135∘ (как смежные)
⇒∠FDA=180∘−∠CBD−45∘+∠CBD=135∘−∠EDB+∠CBD=135∘−∠ECA−∠CBD+∠CBD=135∘−∠ECA=∠EDB
Имеем, что ∠FDE=∠EDB⇒DE - биссектриса ∠FDB
Б) Из △AFD по теореме синусов: FDsin(∠FAD)=AFsin(∠ADF)=ADsin(∠DFA)=2Rv2⇒AFsin(∠ADF)=Rv2
2sin(∠ADF)=2Rv2⇒Rv2=1sin(∠ADF)
△FDA=△BDC (по стороне и двум прилежащим углам, CD - общая)
⇒BC=FC;DC=AF+AC=2+6=8
Из △ABC по теореме синусов: ACsin(∠CBD)=CBsin(∠BAC)=ABsin(∠ACB)=2Rv1⇒ACsin(∠CBD)=CBsin(∠BAC); ⇒6sin(∠CBD)=28√2⇒sin(∠CBD)=3√28
⇒cos(∠CBD)=√1−9⋅264=√488
В пункте а) показывалось, что ∠ADF=45∘−∠CBD
⇒sin(∠ADF)=sin(45∘−∠CBD)=sin(45∘)cos(∠CBD)−cos(45∘)sin(∠CBD)=√22⋅√468−√22⋅3√28=2√23−62⋅8=√23−38
и Rv2=8√23−3=8(√23+3)23−9=24+8√2314=12+4√237
Ответ: 12+4√237
Найдите все значения параметра а, при каждом из которых уравнение 2sinx+4sinx+√sinx+2=a⋅log2(161+sinx) не имеет корней.
Пусть t=sinx, −1≤t≤1
2t+4t+√t+2=a⋅log2(161+t), ОДЗ: t≥0⇒0≤t≤1
Рассмотрим на участке t∈[0;1]:
f(t)=2t+4t+√t+2 - монотонно возрастает при t∈[0;1]
fmin=f(0)=1+0+0+2=3
fmax=f(1)=2+4+1+2=9
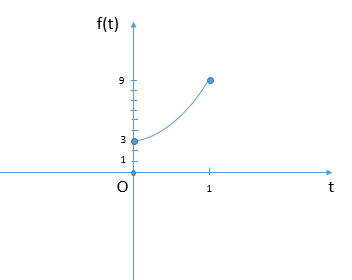
Рассмотрим h(t)=alog2(161+t) на участке t∈[0;1]
При a≥0 h(t) неотрицательна при t∈[0;1] и монотонно убывающая
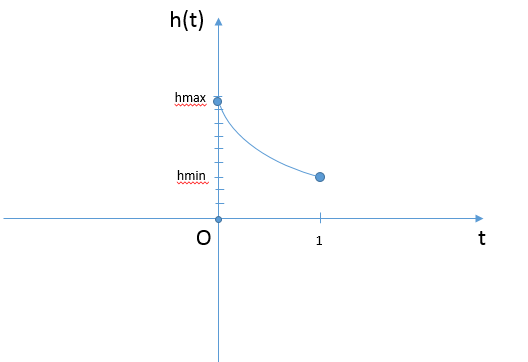
Тогда
hmin=h(0)=alog2(161+0)=4a
hmax=h(1)=alog2(161+1)=3a
При a<0 график h(x) полностью лежит в нижней полуплоскости.
Рассмотрим уравнение при a<0, тогда графическое решение:
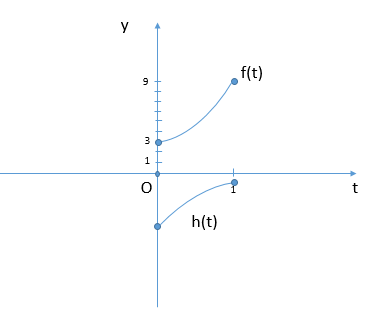
Откуда следует, что при a<0 уравнение не имеет решений!
Рассмотрим уравнение при a≥0, тогда его графическое решение:
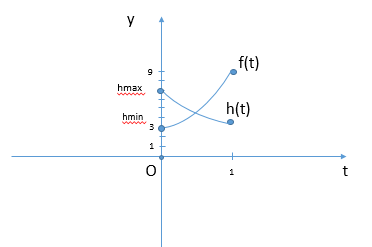
Откуда следует, что
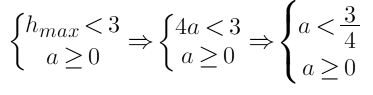
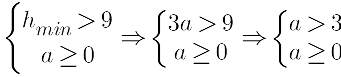
Объединение решений: a∈(−∞;34)∪(3;+∞)
Ответ: (-∞; 0,75)⋃(3; +∞)
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||