Вариант 1
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
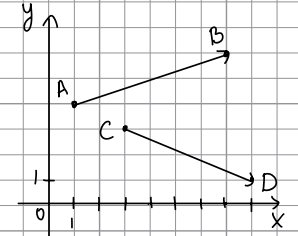
Найдите площадь ромба ABCD (в см2), если известно, что CD = 5, а BD = 8 см.
На мероприятие было закуплено 13 синих, 11 красных, 6 жёлтых и 20 белых футболок. Какова вероятность того, что Саше достанется красная футболка?
В сборнике билетов по физике всего 40 билетов, в 8 из них встречается вопрос по теме «Радиоактивность».
Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Радиоактивность».
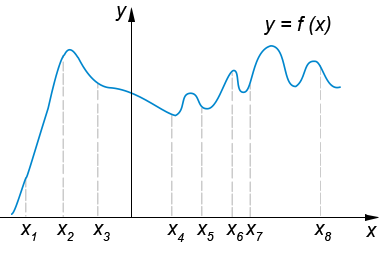
На рисунке изображён график функции y=f(x) и восемь точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) отрицательна?
На нагревание 5 кг воды потребовалось количество теплоты, равное 1 890 000 Дж, которое можно рассчитать по формуле Q=cm(t2−t1), где Q — количество теплоты, c — удельная теплоемкость вещества, m — масса вещества, t1 — начальная температура, t2 — конечная температура вещества. До какой температуры (в °С) нагрелась вода, если удельная теплоемкость воды равна 4200Джкг⋅∘С, а ее начальная температура 1°С?
Из города А в город В в одно и то же время выехали два автомобиля. Расстояние между городами 350 км. Второй автомобиль проехал с постоянной скоростью и без остановок весь путь. Первый автомобиль проехал первую половину пути, затем сделал остановку на 1 час, после чего продолжил путь с прежней скоростью. В итоге первый автомобиль прибыл в город В на 3 часа позже, чем второй. Найдите скорость второго автомобиля, если известно, что она больше скорости первого на 20 км/ч. Ответ дайте в км/ч.
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите точку минимума функции y=(x−5)ex+2
Найдем производную и точки, в которых она равна 0 или не существует, разобьем ими область определения функции на отрезки и определим знаки производной на них. Переход знака производной с отрицательного значения в положительное будет точкой минимума
y=(x−5)ex+2
y′=((x−5)ex+2)′=ex+2+(x−5)ex+2=(x−4)ex+2
y'=0 при x=4. При х<4 производная отрицательная, при x>4 производная положительная, значит x=4 — точка минимума
Дано уравнение √x=√[x]+√{x}, где [a] — целая часть числа а, т.е. наибольшее целое число, не превосходящее а; {a} — дробная часть числа а, т.е. {a} = а - [a].
А) Решите уравнение.
Б) Найдите его корни, принадлежащие отрезку [tgπ12;tg5π12].
А) Преобразуем уравнение:
√x=√[x]+√x−[x]Так как левая и правая части уравнения неотрицательны, возведем в квадрат обе части уравнения. Получим :
x=[x]+2√[x]x−[x]2+x−[x]
2√[x]x−[x]2=0
[x]x−[x]2=0
[x](x−[x])=0
Имеем два случая:
1 случай:
[x]=0
т.е. целая часть равна 0. Имеем
0≤x<1
2 случай:
x−[x]=0
x=[x]
т.е. число-целое,дробной части нет,x∈N
Б) Преобразуем tg:
tgπ12=√1−cosπ61+cosπ6=√1−√321+√32=√(1−√32)21−34=1−√3212=2(1−√32)≈0.3
tg5π12=√1−cos5π61+cos5π6=√1+cosπ61−cosπ6=1+√3212=2(1+√32)≈3.7
Имеем,что в промежуток 0≤x<1 входит [tgπ12;1)
В промежуток x∈N входит x=1;2;3
Ответ: A) 0≤x<1 или x∈N
Б) [tgπ12;1]∪{2;3}
В пирамиде SABC угол ASB равен 60°, а углы BSC и CSA - по 45°.
А) Докажите, что плоскости BSC и ASC перпендикулярны.
Б) Найдите радиус сферы вписанной в пирамиду SABC, если известно, что SA=SB=2, SC=2√2.
Дано:
SABC -пирамида, ∠ASB=60∘,,∠BSC=∠CSA=45∘, r-радиус вписанной в пирамиду сферы
SA=SB=2,SC=2√2
Доказать: (BSC)⊥(ASC)
Найти: r
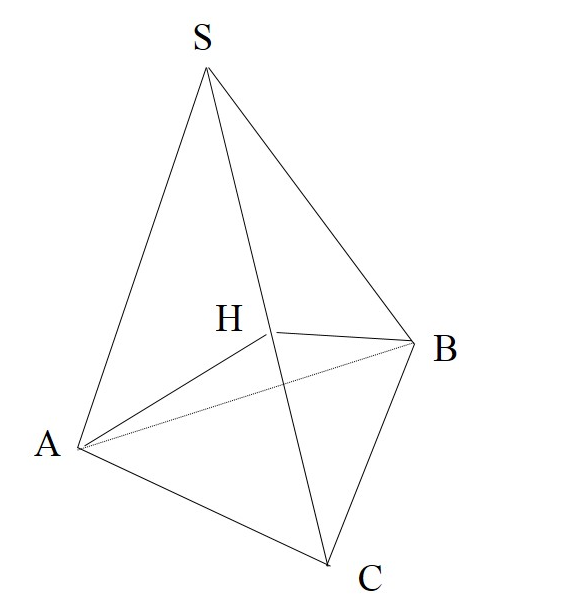
Решение:
1) т.к. AS=SB, то треугольник ASB-равнобедренный.Следовательно, ∠SAB=∠SBA=180∘−60∘2=60∘. Т.к. все углы треугольника равны 60,то треугольник ASB-равносторонний, т.е. AC=CB=AB
△ASC=△BSC (по первому признаку равенства треугольников, т.к. AS=CB,∠ASC=∠CSB, SC-общая). Следовательно, AC=BC.
△SCB: по теореме косинусов имеем, что BC2=SC2+BS2−2∗SC∗BS∗cos(∠CSB)
BC2=8+4−2∗2√2∗2∗√22 ⇒BC2=4⇒BC=2
т.е. BC=AC=2,SB=AS=2. Следовательно △ASC,△SCB-равнобедренные⇒∠SCA=∠SCB=45∘⇒∠SAC=∠SBC=90∘
Проведем BH⊥ SC, то есть высоту в треугольнике ASC. Имеем, что AH-высота треугольника BSC. т.е. BH⊥SC,AH⊥SC.Имеем по определению двугранный угол AHB,причем в треугольнике AKB AH=HB=√2. По теореме косинусов найдем ∠AHB и получим,что ∠AHB=90∘ . Следовательно и двугранный угол AHB=90∘, т.е. искомые плоскости перпендикулярны, что и требовалось доказать
2) Чтобы найти радиус вписанной сферы, воспользуемся следующей формулой: r=VпирSполн
Найдем объем пирамиды: Vпир=13SSBC×AH=13×(12×2×2)×√2=2√23
Найдем площадь всей поверхности пирамиды:Sполн=2×SASB+2×SASC=2×4√34+2×12×2×2=2√3+4
r=3×2√23×(2√3+4)=√2(√3−2)3−4=√8−√6
Ответ:√8−√6
Решите неравенство 4x+16x2≥5⋅2x+1x.
4x+16x2≥5×2x+1x
22x+16x2≥10×2xx
Домножим обе части на x2xПолучим 2 случая :
1 сл: x>02x×x+162x×x≥10
Пусть y=2x×x. Тогда
y+16y≥10
y2+16−10yy≥0
Нули числителя: y2+16−10y=0
D=100−16⋅4=100−64=36
y1=8,y2=2
Нули знаменателя:y=0
Нанесем значения на числовую прямую и определим знаки:
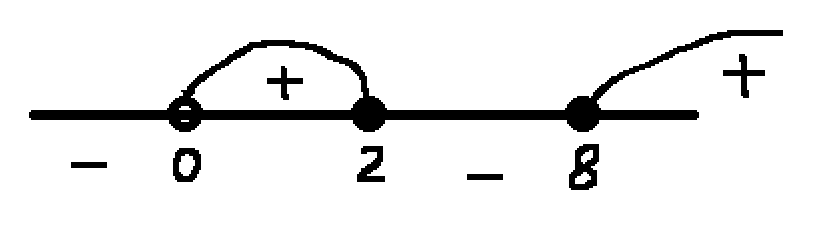
Найдем значения x в точках на концах полученных промежутков. Получим, при y=0 x=0, y=2, x=1, y=8,x=2. Получаем следующие промежутки:
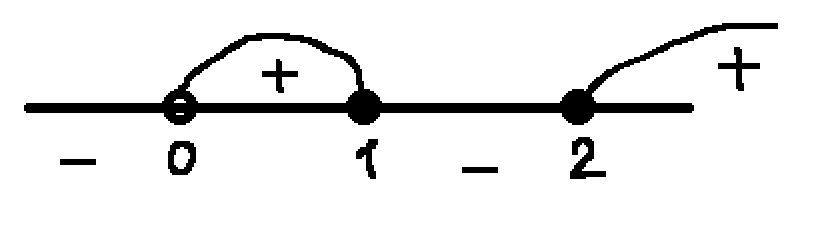
С учетом того, что x>0, получим промежутки (0;1]⋃[2;+∞)
2 сл: x<0 y2+16−10yy≤0
Нанесем значения на числовую прямую и определим знаки:
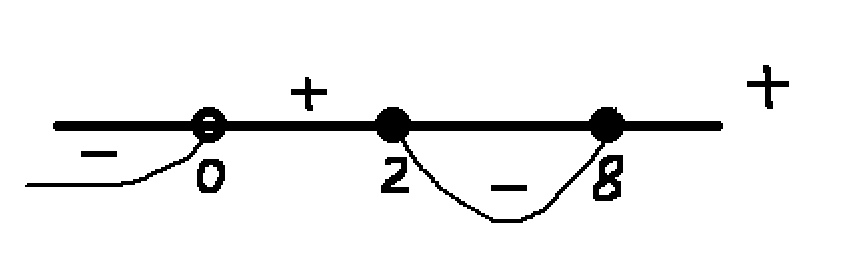
Найдем значения x в точках на концах полученных промежутков. Получим, при y=0 x=0, y=2, x=1, y=8,x=2. Получаем следующие промежутки:
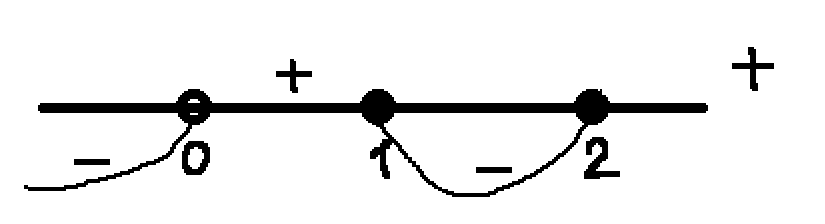
При этом учтем, что в данном случае x<0 Получим промежуток (-∞;0)
Ответ: (-∞;0)⋃(0;1]⋃[2;+∞)
Накануне Нового года Деды Морозы раскладывали равными количествами конфеты в подарочные пакеты, а эти пакеты складывали в мешки, по 2 пакета в один мешок. Те же самые конфеты они могли разложить в пакеты так, что в каждом из них было бы на 5 конфет меньше, чем раньше, но тогда в каждом мешке стало бы лежать по 3 пакета, а мешков при этом потребовалось бы на 2 меньше. Какое наибольшее количество конфет могли раскладывать Деды Морозы?
Пусть x- количество конфет в одном пакете, а y- количество мешков.Тогда в первом случае 2xy, а во втором случае-3(x−5)(y−2). Так как было одинаковое количество конфет, то получим уравнение: 2xy=3(x−5)(y−2). Преобразуем: (x−15)(y−6)=60. Т.е множители должны быть натуральными числами и в произведении давать число 60. При переборе должны получить числа 1 и 60, 2 и 30, 3 и 20 и тд. После перебора, получим,что максимальное xy получаем при значениях множителей 1 и 60, то есть x=16, y=66. т.е. получаем общее количество конфет 2xy=2*16*66=2112.
Ответ: 2112
А) На координатной плоскости Оху изобразите фигуру, заданную неравенством
logx2+y2(x+y)>1.
Б) Найдите площадь полученной фигуры.
ОДЗ:
x+y>0; y>−x
x2+y2>0 всегда, кроме x=0; y=0
x2+y2≠1. Окружность с центром О1(0;0) и радиусом R=1. Изображаем пунктиром.
Преобразуем правую часть уравнения: 1=logx2+y2(x2+y2)
Тогда получим:
logx2+y2(x+y)>logx2+y2(x2+y2)
1 сл: x2+y2>1
x+yx2+y2>1
x+y−x2−y2x2+y2>0
−x−y+x2+y2x2+y2<0
−x−y+x2+y2<0
(x−12)2+(y−12)2<12
Окружность с центром в точке (1/2;1/2) и радиусом R=1√2 при x2+y2>1
2 сл: 0<x2+y2<1
x+yx2+y2<1
x+y−x2−y2x2+y2<0
−x−y+x2+y2x2+y2>0
−x−y+x2+y2>0
(x−12)2+(y−12)2>12
Окружность с центром в точке (1/2;1/2) и радиусом R=1√2 при 0<x2+y2<1
Изобразим на графике:
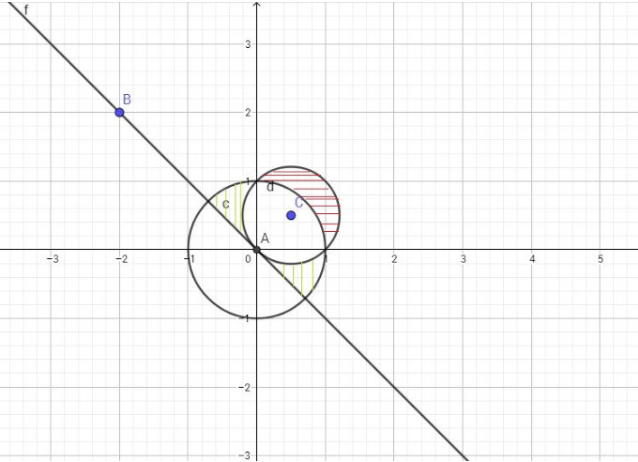
Найдем площадь полученной фигуры:
Sgreen=12Sбольшойокр−(12Sмалойокр+(14Sбольшой−Sпрямоугтреуг)=π2−(π4+(π4−12)=12
Sred=12Sмалойокр−(14Sбольшой−Sпрямоугтреуг)=π4−(π4−12)=12
Sполн=Sgreen+Sred=12+12=1
Ответ:1
Для каждого значения параметра а найдите наибольшее значение функции f(x)=(|x|−6)⋅x2+3|x|⋅(3−a2)+6ax на отрезке [-3; 3].
Имеем два случая: x<0,x≥0
1 случай: x≥0. Преобразуем функцию:
f(x)=x3−6x2+(9+6a−3a2)x
Найдем производную функции:
f′(x)=3x2−12x+(9+6a−3a2)
f′(x)=0
x2−4x+3+2a−a2=0
D=16−4(3+2a−a2)=4(a−1)2
x1=3−a, x2=1+a
Определим знак производной:
1) 0<a<1; 1<a+1<2; 2<3-a<3
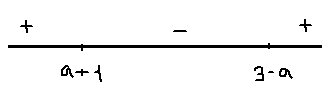
x=a+1- точка максимума;fmax=
fmax=f(a+1)=−2(a+1)(a2−a−2)
2) 1<a<2; 2<a+1<3;1<3-a<2
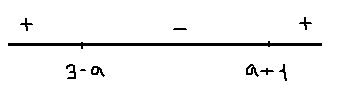
x=3-a-точка максимума
fmax=f(3−a)=2(3−a)(6−a)
3)2<a<3; 3<a+1<4; 0<3-a<1
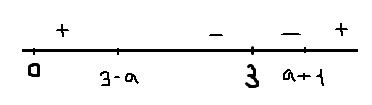
x=a+1 не принадлежит отрезку x=3-a- точка максимума
4)a>3
x=a+1,x=3-a не принадлежат отрезку значений x
т.к. функция убывает, то fmax=f(0)=0
2 случай: x<0. Преобразуем функцию:
f(x)=−x3−6x2+(−9+6a+3a2)x
Найдем производную функции:
f′(x)=−3x2−12x+(−9+6a+3a2)
f′(x)=0
x2+4x+3−2a−a2=0
D=16−4(3−2a−a2)=4(a+1)2
x1=−3−a, x2=−1+a
Определим знак производной:
1) -1<a<0;-3<-3-a<-2; -2<a-1<-1
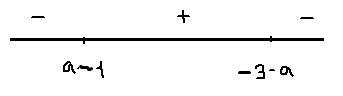
x=a-1- точка максимума;fmax=
fmax=f(a−1)=−2(a−1)(a2+2a+2)
2) -2<a<-1; -3<a-1<-2;-2<-3-a<-1
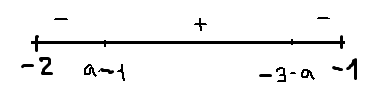
x=-3-a-точка максимума
fmax=f(−3−a)=2a(−3−a)(a+3)
3)-3<a<-2; -4<a1<-3;
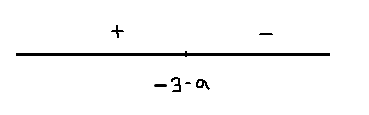
x=-3-a точка максимума
fmax=f(−3−a)=2a(−3−a)(a+3)
4)a<-3; a-10
т.к. функция убывает, то fmax=f(−3)=−9a2−18a
Ответ:
при a≤-3 fmax=–9a2–18a;
при -3<a≤-1 fmax=-2a(a+3)2;
при -1<a≤0 fmax=2·(a–1)·(a2+2a+2);
при 0<a≤1 fmax=(a+1)·(–2a2+2a+4));
при 1<a≤3 fmax=2·(3–a)·(6–a);
при a>3 fmax=0.
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||