Решение:

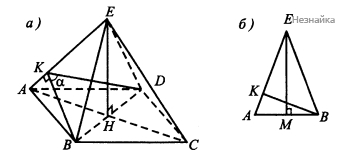
а) Рассмотрим правильную четырехугольную пирамиду $\mathrm{EABCD}$ и построим сечение, проходящее через вершины $\mathrm B$ и $\mathrm D$, перпендикулярное ребру $\mathrm{AE}$. Проведем $\mathrm{BK}\perp\mathrm{AE}$ и докажем, что $DK\perp AE$ (см. рисунок (а) )

В треугольниках $AKB$ и $AKD$ сторона $AK$ - общая, $AB=AD$ и $\angle BAK=\angle DAK$. Следовательно $\bigtriangleup AKB=\bigtriangleup AKD$ по первому признаку равенства треугольников. Поэтому $\angle AKB=\angle AKD=90^\circ$. Значит, $AE\perp DK$ и $AE\perp$ плоскости $BKD$. Таким образом, $BKD$ - искомое сечение.

б) Пусть $EH$ - высота пирамиды $EABCD$.

$AC=BD=AB\sqrt2=18\sqrt2$, $AH=\frac12AC=9\sqrt2$ $AE=\sqrt{AH^2+EH^2}=\sqrt{(9\sqrt2)^2+24^2}=\sqrt{738}$

Рассмотрим равнобедренный треугольник $ABE$ (см. рисунок (б)). Апофему $EM$ найдем из $\bigtriangleup MBE$, учитывая, что $MB=\frac12AB=9$.

$EM=\sqrt{BE^2-MB^2}=\sqrt{738-81}=\sqrt{657}$

найдем высоту $BK$ из формулы площади $\bigtriangleup AEB$.

$S_{AEB}=\frac12EM\times AB=\frac12EA\times BK$

Отсюда $BK=\frac{EM\times AB}{EA}=18\frac{\sqrt{657}}{\sqrt{738}}$

Так как $\bigtriangleup AKB=\bigtriangleup AKD$, то $DK=BK$. По теореме косинусов для $\bigtriangleup BKD:$ $BD^2=DK^2+BK^2-2DK\times BK\times\cos\alpha$, где $\alpha=\angle BKD$ - угол между смежными боковыми гранями.

$\begin{array}{l}\left(18\sqrt2\right)^2=\frac{657\times18^2}{738}\times2\times(1-\cos\alpha)\\\cos\alpha=-\frac9{73}\end{array}$

Ответ: $-\frac9{73}$