Решение:

Рассмотрим $\bigtriangleup MNP$:

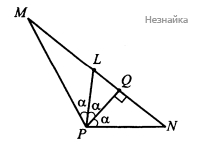
В $\bigtriangleup LPN$ высота $PQ$ является также биссектрисой, значит, $\bigtriangleup LPN$ равнобедренный, PQ - медиана и $LQ=QN=\frac14MN$. В $\bigtriangleup MPQ\;\;PL\;-\;$ биссектриса, тогда $\frac{PQ}{MP}=\frac{LQ}{ML}=\frac12,$ следовательно $\bigtriangleup MPQ$ - прямоугольный с гипотенузой $MP$, тогда $\angle QMP=30^\circ$, $\angle MPQ=60^\circ$, $2\alpha=60^\circ\;=>a=30^\circ.$

Итак $\bigtriangleup MNP$ - прямоугольный с гипотенузой $MN$ и острым углом $30^\circ$.

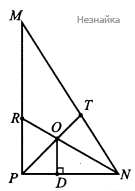
б) Пусть $O$ - центр вписанной окружности, $PT,\;NR$ - биссектрисы, $OD=r$ - радиус вписанной окружности.

$\angle OPD=45^\circ$, тогда $PD=OD=r$. $\angle OND=\frac12\angle MNP=30^\circ$ тогда $ND=OD\sqrt3=r\sqrt3$, $NP=r+r\sqrt3=r(\sqrt3+1)$. $MP=NP\sqrt3=r\sqrt3(\sqrt3+1)$

$S_{MNP}=\frac12MP\times NP=\frac12r^2\sqrt3(\sqrt3+1)^2$

По условию $S_{MNP}=6+4\sqrt3$

$\begin{array}{l}\frac12r^2\sqrt3(\sqrt3+1)^2=6+4\sqrt3\\r=\sqrt2\end{array}$

Ответ: $\sqrt2$