В треугольнике $A_1B_1C_1$ проведем высоту $A_1H$. Заметим, что $BB_1\perp(A_1B_1C_1)$, так как высота прямой призмы перпендикулярна плоскости основания. Тогда $BB_1\perp A_1H$, поскольку прямая $A_1H$ лежит в плоскости $(A_1B_1C_1)$. Тогда $A_1H\perp(CC_1B)$ по признаку перпендикулярности прямой и плоскости. Отсюда по признаку перпендикулярности плоскостей следует, что $(BHA_1)\perp(CC_1B)$, так как плоскость $(A_1B_1C_1)$ содержит прямую, перпендикулярную плоскости $(CC_1B)$. Значит $\bigtriangleup BHA_1$ - искомое сечение.

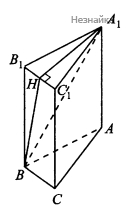
б) Так как $A_1H\perp(CC_1B_1)$, $BH$ является проекцией $BA_1$ на плоскость $(CC_1B_1)$, а значит искомый угол равен углу $HBA_1$. $A_1H$ - высота равнобедренного треугольника, проведенная к основанию, значит, $A_1H$ - медиана, $B_1H=\frac12B_1C_1=\frac12BC=5$. $BH=\sqrt{BB_1^2+B_1H^2}=\sqrt{33+25}=\sqrt{58}$, так как $A_1B_1=AB$. В прямоугольном треугольнике $AA_1B$ по теореме Пифагора $A_1B=\sqrt{AB^2+AA_1^2}=\sqrt{256+33}=17$. $\cos\angle HBA_1=\frac{HB}{A_1B}=\frac{\sqrt{58}}{17}$

Ответ: $\frac{\sqrt{58}}{17}$