Решение:

а) Не нарушая общности, можем считать, что большая окружность вписана в угол $AOC$. Пусть $CQ=r;\;PC=4r$. так как окружность с центром $P$ вписана в угол $AOC$, то $PA\perp OA,\;PC\perp OC,\;OA=OC$ как отрезки касательных, проведенные из одной точки. аналогично $OC=OB$, тогда $OA=OB$, что и требовалось доказать.

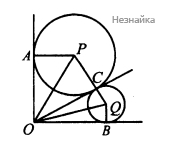
б) Из того, что $PO$ и $QO$ - биссектрисы углов $AOC$ и $BOC$ соответственно, следует, что $\angle POQ=45^\circ$

Обозначим $OA=OB=OC=x$, тогда $OP=\sqrt{16r^2+x^2\;},\;OQ=\sqrt{r^2+x^2},\;PQ=4r+r=5r$. Учитывая, что $\angle POQ=45^\circ,$ по теореме косинусов имеем $PQ^2=OP^2+OQ^2-2OP\times OQ\times\frac{\sqrt2}2$

$16r^2+x^2+r^2+x^2-\sqrt2\sqrt{16r^2+x^2}\sqrt{r^2+x^2}=25r^2$, решая уравнение относительно $x^2$ , получим $x^2=\frac{33\pm5\sqrt{41}}2r^2$

$\cos\angle COQ=\frac{OC}{OQ}=\frac x{\sqrt{r^2+x^2}}=\sqrt{\frac{33\pm5\sqrt{41}}{35\pm5\sqrt{41}}}.$

Если $\cos\angle COQ=\sqrt{\frac{33-5\sqrt{41}}{35-5\sqrt{41}}}.$, то $\cos\angle BOC=\cos(2\angle COQ)=2\cos^2\angle COQ-1=2\times\frac{33-5\sqrt{41}}{35-5\sqrt{41}}-1=\frac{31-5\sqrt{41}}{35-5\sqrt{41}}<0$, что противоречит тому, что $\angle BOC<90^\circ$

Если $\cos\angle COQ=\sqrt{\frac{33+5\sqrt{41}}{35+5\sqrt{41}}},$ то $\cos\angle BOC=\cos(2\angle COQ)=2\cos^2\angle COQ-1=2\times\frac{33+5\sqrt{41}}{35+5\sqrt{41}}-1=\frac{3+\sqrt{41}}{10}$

Ответ: $\frac{3+\sqrt{41}}{10}$.