Решение:

а) Не нарушаю общности, можем считать, что большая окружность вписана в угол $AOC$. Пусть $CQ=r,\;PC=3r$ (см. рисунок). Так как окружность с центром $P$ вписана в угол $AOC$ , то $PA\perp OA,\;PC\perp OC,\;OA=OC$ как отрезки касательных, проведенные из одной точки. Тогда $\bigtriangleup PAO=\bigtriangleup PCO$ и значит $\angle AOP=\angle COP$. Аналогично $\angle COQ=\angle BOQ$. Отсюда $\angle POQ=\angle POC+\angle QOC=\frac12\angle AOC+\frac12\angle BOC=\frac12\angle AOB=45^\circ$. Тем самым доказано утверждение пункта а

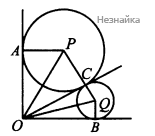
б) Обозначим $OA=OC=OB=x$. Тогда $OP=\sqrt{9r^2+x^2}$, $OQ=\sqrt{r^2+x^2}$. $PQ=3r+r=4r$. Учитывая, что $\angle POQ=45^\circ$ по теореме косинусов $PQ^2=OP^2+OQ^2-2OP\times OQ\times\frac{\sqrt2}2$

$9r^2+x^2+r^2+x^2-\sqrt2\sqrt{9r^2+x^2}\times\sqrt{r^2+x^2}=16r^2$

$x^2=(11\pm4\sqrt7)r^2$

$\cos\angle COQ=\frac{OC}{OQ}=\frac x{\sqrt{r^2+x^2}}=\sqrt{\frac{11\pm4\sqrt7}{12\pm4\sqrt7}}$

Если $\cos\angle COQ=\sqrt{\frac{11-4\sqrt7}{12-4\sqrt7}}$, то $\cos\angle BOC=\cos(2\angle COQ)=\frac{5-2\sqrt7}{6-2\sqrt7}<0$, что противоречит тому, что $\angle BOC<90^\circ$

Если $\cos\angle COQ=\sqrt{\frac{11+4\sqrt7}{12+4\sqrt7}}$, то $\cos\angle BOC=\cos(2\angle COQ)=\frac{1+\sqrt7}4$

Ответ: $\frac{1+\sqrt7}4$.