Задание № 8186
Две окружности с центрами О и О1 радиусы которых 2 и 6, касаются внешним образом, АС — их общая внешняя касательная.
а) Докажите, что угол СО1О равен 60°, где О1С — радиус, проведённый в точку касания.
б) Найдите периметр фигуры, образованной внешними касательными и внешними дугами окружностей.
Решение:
а) Заметим, что OA⊥AC и O1C⊥AC по свойству радиусов, проведеных в точку касания (см. рисунок). Опустим OK⊥O1C, тогда OACK - прямоугольник, CK=OA=2,O1K=O1C−CK=6−2=4. Обозначим буквой M точку касания окружностей, тогда OM=2,O1M=6,OO1=8. В прямоугольном треугольнике O1OK выполняется соотношение O1KOO1=12, следовательно, ∠O1OK=30∘. Тогда ∠OO1K=90∘−∠O1OK=60∘,∠CO1O=60∘, что и требовалось доказать.
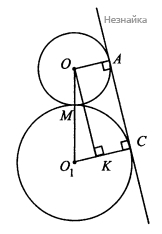
б) ∠O1OA=180∘−600=120∘. Градусная мера внешней дуги внешней окружности равна360∘−120∘−120∘=120∘. Градусная мера внешней дуги большей окружности равна 360∘−60∘−60∘=240∘. Значит, длина внешней внешней дуги меньшей окружности равна 2π×2×120∘360∘=4π3. Длина внешней дуги большей окружности равна 2π×6×240∘360∘=8π. Из треугольника O1OK по теореме Пифагора OK=√OO21−O1K2=√48=4√3. AC=A1C1=4√3
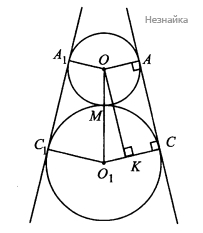
Искомый периметр равен: 4π3+4√3+8π+4√3=8√3+28π3
Ответ: 28π3+8√3
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.