Решение:

Не нарушая общности, можем считать, что $\angle С=90^\circ$. Найдем катет $AC$ прямоугольного треугольника $ABC$: $\frac{BC}{AC}=tgA;\;AC=\frac{BC}{tgA}=\frac3{\sqrt3}=\sqrt3$

Угол между плоскостью ABC и плоскостью основания усеченного конуса равен углу $CAC_1$, где $C_1C$ - перпендикуляр к плоскости основания конуса (см. рисунок).

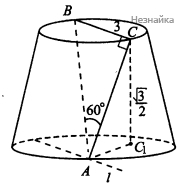
Действительно, плоскость $ABC$ пересекает плоскость верхнего основания конуса по прямой $BC$, а нижнего основания конуса по прямой $l$, значит $l\parallel BC$. Так как $AC\perp BC$, то $AC\perp l$. $AС_1$ - проекция $AC$ на плоскость нижнего основания конуса, следовательно, $AC_1\perp l$ по теореме о трех перпендикулярах. $\angle CAC_1$ найдем из прямоугольного треугольника $ACC_1$. $\sin\angle CAC_1=\frac{CC_1}{AC}=\frac12$, $\angle CAC_1=30^\circ$.

Ответ: $30^\circ$