Решение:

а) Рассмотрим случай, когда прямые $BC$ и $O_1O_2$ не совпадают. Тогда $\bigtriangleup O_2AC$ и $\bigtriangleup O_1AB$ - равнобедренные и, следовательно, $\angle O_2AC=\angle O_2CA,\;$$\angle O_1AC=\angle O_1BC\;$, но $\angle O_2AC$ - общий, поэтому $\angle O_2AC=\angle O_1AC=\angle O_1BC=\angle O_2CA$ и $\bigtriangleup O_2AC\;\sim\;\bigtriangleup O_1AB$ по двум углам и $\frac{AC}{AB}=\frac{AO_2}{AO_1}$

$\begin{array}{l}\frac{BC}{AB}=\frac{AB-AC}{AB}=1-\frac{AC}{AB}\\\frac{O_1O_2}{AO_1}=\frac{AO_1-AO_2}{AO_1}=1-\frac{AO_2}{AO_1}\end{array}$

Значит, $\frac{BC}{AB}=\frac{O_1O_2}{AO_1}$ или $\frac{BC}{O_1O_2}=\frac{AB}{AO_1}$ (см. рисунок)

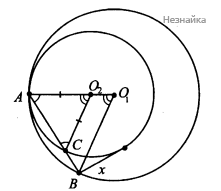
Рассмотрим случай, когда прямые $O_1O_2$ и $AB$ совпадают:

$\frac{AB}{AO_1}=2;$$BC=AB-AC=10-8=2$; $O_1O_2=AO_1-AO_2=1$; $\frac{BC}{O_1O_2}=2=\frac{AB}{AO_1}$ (см. рисунок)

б) Обозначим $x$ - искомая длина касательной, тогда $\begin{array}{l}x^2=AB\times BC=AB^2\times\frac{O_1O_2}{AO_1}=\frac15\\x=\frac{\sqrt5}5\end{array}$

Ответ: $x=\frac{\sqrt5}5$