Решение:

а) В трапеции $ABCD$ треугольники $AOD$ и $BOC$ подобны, поскольку $\angle OAD=\angle OCB$ и $\angle ODA=\angle OBC$ как накрест лежащие при параллельных прямых $AD$ и $BC$ и секущих $AC$ и $BD$ соответственно (см. рисунок)

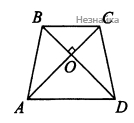
Значит, $\frac{AO}{CO}=\frac{DO}{BO}$. Умножая почленно это равенство на равенство $AO\times CO=BO\times DO$ из условия задачи, получим $AO^2=DO^2$. Отсюда $AO=DO$, $BO=CO$ и треугольники $AOB$ и $DOC$ равны по первому признаку. Следовательно $AB=CD$

б) Т.к. Трапеция $ABCD$ равнобедренная, то вокруг нее можно описать окружность. обозначим ее радиус через $R$.

Треугольники $AOD$ и $BOC$ - равнобедренные и прямоугольные. Значит $\angle OAD=45^\circ$ и $CO=\frac{BC}{\sqrt2}$, $DO=\frac{AD}{\sqrt2}$. По теореме синусов для треугольника ACD имеем: $\frac{CD}{\sin\angle CAD}=2R,\;R=\frac{CD}{\sqrt2}$

$CD^2=CO^2+DO^2=\frac12(AD^2+BC^2)=50$

Отсюда $CD=5\sqrt2$ и R=5

Ответ: 5