Задание № 7918
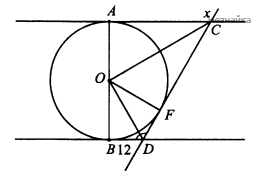
К окружности с центром О проведены три касательные ,две из которых АС и BD-параллельны А и В -точки касания. Третья касательная пересекает их в точках C и D соответственно, а также касается окружности в точке F.
а) Докажите ,что произведение отрезков касательных ,отсекаемых третьей касательной на двух параллельных касательных ,равно квадрату радиуса т.е. AC ∗ BD = AO2
б) Найдите площадь четырехугольника ABCD, если BD=12, ∠BDF=120°
Решение:
а) Доказать, что AC×BD=AO2 (см. рисунок)
ABCD - прямоугольная трапеция, так какAB⊥AC,AB⊥BD.
CO - биссектриса ∠ACF
DO - биссектриса ∠BDF
Тогда ∠COD=90∘, на основании теоремы о биссектрисах внутренних односторонних углов при параллельных прямых AC∥BD и секущей CD. OF⊥CD. Высота OF, проведенная из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, то есть OF2=CF×FD. OF=OA (как радиусы), CF=AC, FD=BD (как отрезки касательных, проведенные к окружности из одной точки).
OA2=AC×BD, что и требовалось доказать.
SABDC=12(AC+BD)×AB.. В силу того, что AB=2AO,AC=BD=CF+FD=CD, получаем SABDC=AO×CD
△BOD: ∠OBD=90∘;∠ODB=60∘;OB=12tg60∘=12√3
△AOC:∠OAC=90∘∠OCA=30∘
AC=OA×ctg(30∘)=12√3√3=36
CF=AC=36,FD=BD=12 CD=36+12=48
SABDC=12√3×48=576√3
Ответ: 576√3
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.