Решение:

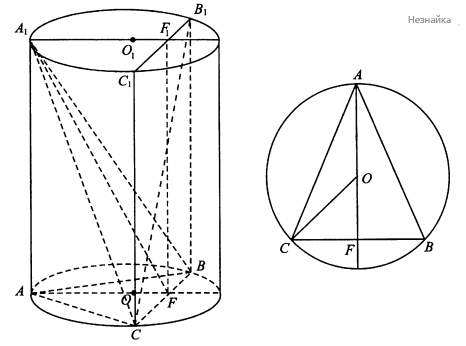
а) Пусть $O$ и $O_1$ - центры оснований цилиндра, тогда $F$ и $F_1$ - середины хорд $BC$ и $B_1C_1$ соответственно (см. рисунок) . Покажем, что $AFF_1$ - искомая плоскость. $A_1F$ - медиана, значит, и высота равнобедренного треугольника $A_1BC$. $FF_1\parallel BB_1$, значит, $FF_1\perp(ABC)$ и, в частности, $FF_1\perp BC$. Так как $FF_1\perp BC$ и $A_1F\perp BC,\;$ $(AFF_1)\perp BC,\;$, откуда $(AFF_1)\perp A_1BC\;$ и $(AFF_1)\perp BB_1C_1C\;$. Сечением призмы $ABCA_1B_1C_1$ плоскостью $AFF_1$ является прямоугольник $AFF_1A_1$

б) Угол между плоскостями $CA_1B$ и $CBB_1$ - это угол $\angle A_1FF_1$

$\bigtriangleup A_1FF_1$ - прямоугольный, $tg\angle A_1FF_1=\frac{A_1F_1}{FF_1}$

$\bigtriangleup ABC$ - равнобедренный (по условию), $CF=\frac{BC}2=5$

$\bigtriangleup COF$ - прямоугольный, $OF=\sqrt{CO^2-CF^2}=\sqrt{15^2-5^2}=10\sqrt2$

$AF=AO+OF=15+10\sqrt2=5(3+2\sqrt2)$$AF=A_1F_1$

$tg\angle A_1FF_1=\frac{5(3+2\sqrt2)}{60}=\frac{3+2\sqrt2}{12}$

Ответ: $arctg\;\frac{3+2\sqrt2}{12}$