Задание № 7913
Найдите все значения параметра а, при которых уравнение (3a−23)sin4x+2a3−1+cos24x=0имеет ровно три корня, расположенных на отрезке [3π4;π]
Решать другие задания по теме: Задачи с параметром
Показать ответ
Комментарий:
 Ответ:
Ответ:
Решение:
(3a−23)sin4x+2a3−1+cos24x=0;
(3a−23)sin4x+2a3−sin24x=0;
sin4x=t,−t2+3a−23t+2a3=0;
t2−3a−23t−2a3=0; t=(3a−2)±(3a+2)6
t1=−23,t2=a

1) sin4x=−23; 2) sin4x=a.
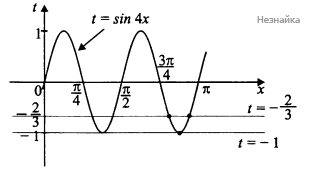
Уравнение sin4x=a имеет на отрезке [3π4;π] один корень при a=−1 и уравнение sin4x=−23 имеет на [3π4;π] два корня (см. рисунок)
Ответ: -1
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.