а) В $\bigtriangleup ABC$ по теореме синусов $\frac{AC}{\sin\angle ABC}=2R,\;AC=2R\sin\alpha$

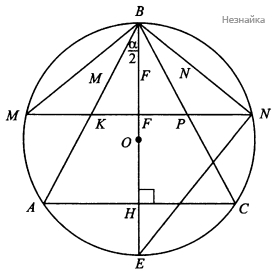
Проведем $BH\perp AC$

По условию $\bigtriangleup ABC$ - равнобедренный, значит высота $BH$ является медианой и биссектрисой $AH=\frac12AC=R\sin\alpha$ (см. рисунок)

$AB=\frac{AH}{\sin{\displaystyle\frac\alpha2}}=\frac{R\sin\alpha}{\sin{\displaystyle\frac\alpha2}}=2R\cos\frac\alpha2$, что и требовалось доказать.

б) В $\bigtriangleup ABH\;tg\angle ABH=\frac{AH}{BH}$, $\;BH=\frac{AH}{tg\angle ABH}=\frac{R\sin\alpha}{tg{\displaystyle\frac\alpha2}}=2R\cos^2\frac\alpha2=2R\cos^230^\circ=\frac32R$

По условию $KP$ - средняя линия $\bigtriangleup ABC$, значит, $BF=\frac12BH=\frac34R.$

$\angle BNE=90^\circ$, как вписанный опирающийся на диаметр, следовательно $\bigtriangleup BNE$ - прямоугольный.

По свойству высоты, проведенной из вершины прямого угла, $NF^2=BF\times FE=\frac34R\times(2R-\frac34R)=\frac{15}{16}R^2$

$NF=\frac{\sqrt{15}R^2}4$, $MN=2NF=\frac{R\sqrt{15}}2$

$\begin{array}{l}S_{MBN}=\frac12MN\times BF=\frac12\times\frac{R\sqrt{15}}2\times\frac34R=\frac{3\sqrt{15}}{16}R^2\\S_{ABC}=\frac12AB\times BC\times\sin\angle ABC=\frac12\times(2R\cos\frac\alpha2)^2\times\sin\alpha=\frac{3\sqrt3}4R^2\\\frac{S_{MBN}}{S_{ABC}}=\frac{3\sqrt{15}R^2}{16}\div\frac{3\sqrt3}4R^2=\frac{\sqrt5}4\end{array}$

Ответ: $\frac{\sqrt5}4$