Решение:

а) Пусть точка $O$ - центр треугольника $ABC$, точки $O_1$ и $O_2$ -центры симметрий граней $AA_1B_1B$ и $BB_1B_1B$. Необходимо построить сечение призмы плоскостью $OO_1O_2$ (См. рисунок).

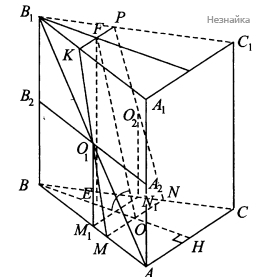
Так как призма правильная, то грани $AA_1B_1B$ и $BB_1C_1C$ равные прямоугольники. Поэтому расстояния от центров $O_1$ и $O_2$ до сторон $AB$ и $BC$ треугольника $ABC$ равны, то есть $O_1M_1=O_2N_1$. Значит, $O_1O_2\parallel M_1N_1$ как противоположные стороны прямоугольника $M_1O_1O_2N_1$. Следовательно прямая $O_1O_2$ параллельна плоскости $ABC$ по признаку параллельности прямой и плоскости.

Плоскость сечения $OO_1O_2$ проходит через прямую $O_1O_2$ и пересекает плоскость $ABC$, следовательно, линия пересечения этих плоскостей параллельна прямой $O_1O_2$. Через точку $O$ проводим прямую $MN$, параллельную $M_1N_1$ . Прямые $MO_1$ и $NO_2$ пересекают плоскость $A_1B_1C_1$ в точках $K$ и $P$ соответственно. Четырехугольник $MKPN$ - искомое сечение

б) По свойству параллельных плоскостей $KP\parallel MN$, следовательно, четырехугольник $MKPN$ - трапеция

$S_{MKPN}=\frac{KP+MN}2\times FO$, где $FO$ - высота трапеции

Точка $O$ является одновременно точкой пересечения медиан и высот треугольника $ABC$, поэтому $MN=\frac23\times AC=\frac23\times6=4,\;BH=3\sqrt3$$BO=\frac23BH=2\sqrt3$

$\bigtriangleup B_1O_1K=\bigtriangleup AO_1M$, так как точка $O_1$ - середина отрезка $AB_1$ и $AB\parallel A_1B_1$

Из равенства треугольников следует $B_1K=AM=\frac13\times6=2.$

Так как $\bigtriangleup KB_1F$ прямоугольный и $\angle B_1KF=60^\circ$, $B_1F=\frac{KB_1\sqrt3}2=\sqrt3$.

$\bigtriangleup KB_1P$ - равносторонний, поэтому $KP=2$

Проведем $FE\perp BH$, тогда $BE=B_1F=\sqrt3$, $OE=OB-BE=2\sqrt3-\sqrt3=\sqrt3$.

По условию $\angle FOE=30^\circ\;$ в прямоугольном треугольнике $FEO$, поэтому $OF=\frac{OE}{\cos30^\circ}=\frac{\sqrt3\times2}{\sqrt3}=2$

$S_{MKPN}=\frac{2+4}2\times2=6$

Ответ: $6$