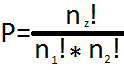
Внашем случае n_z=6

n₁=3(по условию содержат ровно три буквы А)

n₂=3(n_z-n₁=6-3=3)

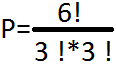
P=(1*2*3*4*5*6)/(1*2*3*1*2*3)=20

Мы нашли количество перестановок с повторениями (для буквы A). У нас остаётся 2 буквы(С, B).

Нужно вычислить количество всех возможных трёхбуквенных слов, состоящих из дух возможных букв(С, B) достаточно сделать следующее 2³(где 3=n₂)

2³=8

20*8=160

Ответ:160