Решение:

ОДЗ:

x-1>0 → x>1

x-1≠1 → x≠2

4^x-1-3⋅2^x-a>0

Введем замену 2^x=t , тогда

1/4t²-3⋅t-a>0

Нули: t₁=6-2√(9+а) , t₂=6+2√(9+а)

t<6-2√(9+а) или t>6+2√(9+а)

1/4t²-3⋅t-a - парабола, ветви которой направленны вверх, так что неравенство 1/4t²-3⋅t-a>0 будет верным и при 9+а<0. Значит, согласно данному условию, a - любое.

x>1 → t>2

x≠2 → t≠4

Преобразуем неравенство: |x - 2|≤ 1

$-1\leq x-2\leq1$

$1\leq x\leq3$

$2\leq t\leq8$

Итого: t≠4, 2<t⩽8

Преобразуем: $\log_{x-1}\left(4^{x-1}-3\cdot2^x-a\right)=0$

$\frac14t^2-3t-a=1$

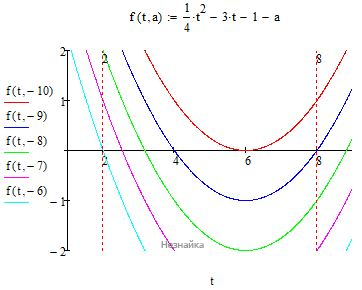
График функции $\frac14t^2-3t-a-1=y(t)$ имеет экстремум в точке t=6 и нули в точках t₁=6-2√(10+а) , t₂=6+2√(10+а).

1) При t₁=t₂=6 - уравнение имеет одно решение в точке касания графика и оси ОХ: а=-10

2) При 2<t⩽8

Корни t₁=6-2√(10+а)>2 расположены слева от экстремума t=6, при этом корни, расположенные справа от экстремума, должны выходить из промежутка t₂=6+2√(10+а)⩾8. Так будет обеспечено наличие одного корня, удовлетворяющего неравенству |x - 2|≤ 1

6-2√(10+а) > 2

а < -6

6+2√(10+а) ⩾ 8

a ⩾ -9

При a=9 имеем два корня t₂=8 и t₁=4, последний не удовлетворяет ОДЗ, поэтому a=9 удовлетворяет условию о наличии одного корня.

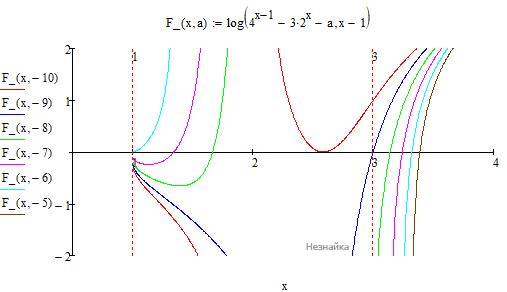
Ответ: $a=-10,\;-9\leq a<-6$