ОДЗ: $x>0$, $x\neq1$, $3x-1>0$

Преобразуем левую часть неравенства:

$log_x(3x-1)(log_x(3x-1)-1)\geq0$

$\frac{ln(3x-1)}{lnx}(\frac{ln(3x-1)-lnx}{lnx})\geq0$

$\frac{ln(3x-1)}{ln^2x}(\frac{ln(3x-1)-lnx}1)\geq0$

Нули числителя: $ln(3x-1)=0$

$3x-1=1$

$x=\frac23$

$ln(3x-1)=lnx$

$3x-1=x$

$2x=1$

$x=\frac12$

Нули знаменателя:

$lnx=0$

$x=1$ - корень кратности 2

Нанесем корни на числовую прямую, учитываю ОДЗ:

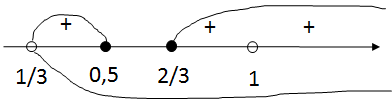
Получаем следующие промежутки: $(\frac13;\;\frac12\rbrack\cup\lbrack\frac23;\;1)\cup\left(1;\;+\infty\right)$

Ответ: $(\frac13;\;\frac12\rbrack\cup\lbrack\frac23;\;1)\cup\left(1;\;+\infty\right)$