Решение:

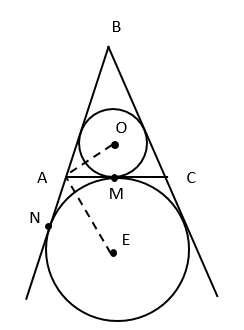
А) $AO$ – биссектриса $\angle BAM$ ( по свойству касательных , проведенных из одной точки)

$AE$ – биссектриса $\angle MAN$

$\angle BAM+\angle MAN=180^\circ$, $2\angle OAM+2\angle MAE=180^\circ$

$\angle OAM+\angle MAE=90^\circ$, т.е. $\bigtriangleup OAE$ – прямоугольный

$AM\perp OM$, т.к. $BM$ – высота,медиана равнобедренного треугольника $\bigtriangleup АВС$

$М$ – середина $АС$

Вторая окружность, также касается $АС$ в точке $М$

$АМ$ – высота $\bigtriangleup АОЕ$, проведенная из прямого угла, значит $АМ=\sqrt{МО\cdot МЕ}$

$АМ=\frac12АС$,$МО=\frac12d_1$, $МE=\frac12d_2$, тогда $\frac12АС=\sqrt{\frac12d_1\cdot\frac12d_1}=\frac12\sqrt{d_1\cdot d_2}$

Б) Пусть $\angle ОАМ=\alpha$, тогда $\angle ВАМ=2\alpha$

Пусть $МЕ=x$, $AM=y$

Из $\bigtriangleup ABM$: $tg2\alpha=\frac{BM}{AM}=\frac8y$

Из $\bigtriangleup OAM$:$tg\alpha=\frac{OM}{AM}=\frac3y$

$tg2\alpha=\frac{2tg\alpha}{1-tg^2\alpha}$

$\frac8y=\frac{2\cdot\frac3y}{1-\frac9{y^2}}$

$\frac8y=\frac{6y}{y^2-9}$

$8(y^2-9)=6y^2$

$8y^2-6y^2=8\cdot9$

$y=6$

$AM=6$

$AM=\sqrt{OM\cdot ME}$

$6=\sqrt{3x}$

$ME=x=12$

Ответ:12