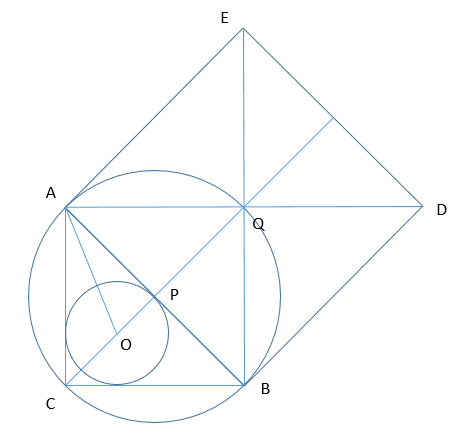
А) Если доказать, что $CQ$ - биссектриса $\angle ACB$, то будет доказано, что $C\in OQ$, т.к. $CO$ - биссектриса $\angle ACB$ (по свойству касательных, проведенных из одной точки)

Рассмотрим четырехугольник $CAQB$:

$\angle C+\angle Q=180^\circ$,$\angle A+\angle B=\angle QAB+\angle QBA+\angle BAC+\angle ABC=180^\circ\Rightarrow CAQB$ может быть вписан в окружность

$\Rightarrow\angle QBA=\angle QCA=45^\circ,\angle QAB=\angle QCB=45^\circ\Rightarrow$(т.к. опираются на равные дуги) $CQ$ - биссектриса $\angle ACB\Rightarrow C\in OQ$, ч.т.д.

Б) $AC=4\sqrt2$, $BC=3\sqrt2$ , $OQ$ - ?

$\bigtriangleup CPB\sim\bigtriangleup APQ$ (по двум углам):$\angle PCB=\angle PAQ=45^\circ$, $\angle CPB=\angle APQ$ как вертикальные $\Rightarrow\angle PBC=\angle PQA$

Пусть $\angle CAB=x$, тогда $\angle ABC=90^\circ-x=\angle PQA$, $\angle QAO=45^\circ+\frac x2$ (т.к. $\angle PAO=\angle CAO$ по свойству касательных)

Тогда для $\bigtriangleup AOQ$: $\angle OQA+\angle QAO+\angle AOQ=180^\circ$

$90^\circ-x+45^\circ+\frac x2+\angle AOQ=180^\circ\Rightarrow\angle AOQ=45^\circ+\frac x2$

$\angle AOQ=\angle QAO\Rightarrow\bigtriangleup AQO$ - равнобедренный, $AQ=OQ=5$

Ответ: 5