А) Предположим, что для произвольной точки плоскости все точки, удаленные от нее ровно на 1 м, другого цвета (если среди них были бы точки того же цвета, то это бы означало, что для этой произвольной точки нашлась точки того же цвета и задача была решена изначально). Следовательно, мы получим окружность радиуса 1 м, центр которой - точка одного цвета, а все точки окружности - точки другого цвета. На окружности всегда найдется хорда, равная радиусу окружности, следовательно мы найдем две точки одного цвета ( на концах хорды), отстоящих друг от друга на длину хорды, т.е. 1м. Ответ : да, можно

Б) Вероятность точки прямой определенного цвета 1/10. Следовательно из 20 точек прямой точки одного цвета попадут минимум 2 раза. Разместим точки разных десяти цветов на одинаковом целочисленном расстоянии друг от друга, тогда 11 точка будет совпадать с цветом любой из предыдущих, так как точки размещены всех 10ти цветов. Значит ответ:да, можно

В) Можно выбрать 4 вершины (вершины одной грани, они не образуют равносторонний треугольник). Если берем пять вершин, то можно составить равносторонний треугольник. На рисунке приведено решение:

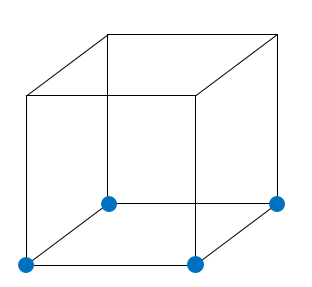
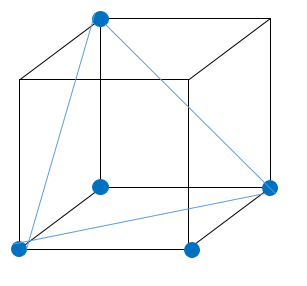
Ответ: А) да; Б) да; В) 4.