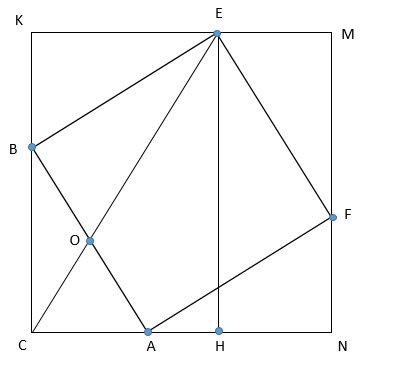
А) Достроим до квадрата $CKMN$ так, чтобы $\bigtriangleup ABC=\bigtriangleup FAN=\bigtriangleup EFM=\bigtriangleup BEK$

Обозначим $\angle OCA=\alpha$ и запишем теорему синусов для $\bigtriangleup OCA$ и $\bigtriangleup OCB$:

$\frac{OC}{sin(\angle OBC)}=\frac{OB}{sinn(90^\circ-\alpha)}$

$\Rightarrow\frac{OA}{OB}\cdot\frac{cos\alpha}{sin\alpha}=\frac{sin(\angle OBC)}{sin(\angle OAC)}$

$\Rightarrow\frac{OA}{OB}=\frac{sin(\angle OBC)}{sin(\angle OAC)}\cdot tg\alpha$

Опустим из Е перпендикуляр на CN. $EH\perp CN;EH=MN=CA+BC=3AC$

$HN=EM$ (по свойству прямоугольника $EMNH$)

$\Rightarrow CH=CN-HN=3AC-AC=2AC$

$\Rightarrow tg(\angle ECH)=tg\alpha=\frac32$

Рассмотрим $\bigtriangleup ABC$: по теореме Пифагора $AB=\sqrt{AC^2+BC^2}=\sqrt{AC^2+4AC^2}=\sqrt5AC$

$sin(\angle ABC)=sin(\angle OBC)=\frac{AC}{\sqrt5AC}=\frac1{\sqrt5}$

$sin(\angle BAC)=sin(\angle OAC)=\frac{2AC}{\sqrt5AC}=\frac2{\sqrt5}$

$\Rightarrow\frac{OA}{OB}=\frac1{\sqrt5}\cdot\frac{\sqrt5}2\cdot\frac32=\frac34$, ч.т.д.

Б) $\frac{S_{\bigtriangleup AOC}}{S_{\bigtriangleup BOE}}-?$

$S_{\bigtriangleup AOC}=\frac12AO\cdot AC\cdot sin(\angle AOC)=\frac12\cdot\frac37AB\cdot AC\cdot\frac2{\sqrt5}=\frac3{7\sqrt5}AC\cdot\sqrt5\cdot AC=\frac37AC^2$

$S_{\bigtriangleup BOE}=\frac12BO\cdot BE=\frac12\cdot\frac47\cdot AB\cdot AB=\frac27\cdot\left(AC\sqrt5\right)^2=\frac{10}7AC^2$

$\Rightarrow\frac{S_{\bigtriangleup AOC}}{S_{\bigtriangleup BOE}}=\frac{\frac37AC^2}{\frac{10}7AC^2}=\frac3{10}$

Ответ: 0,3