Перенесем единицу в левую часть и приведем к общему знаменателю:

$\frac{log_3\sqrt{28\cdot3^x-3}-(x+1)}{x+1}\geq0$

ОДЗ: $28\cdot3^x-3>0$

$x>log_3\frac3{28}$

$x>1-log_328$

Нули числителя: $\frac12log_3(28\cdot3^x-3)-(x+1)=0$

$log_3(28\cdot3^x-3)=2(x+1)$

$28\cdot3^x-3=3^{2(x+1)}$

$9\cdot3^{2x}-28\cdot3^x+3=0$

D=646

$3^x=\frac{28+26}{18}=3\Rightarrow x=1$

$3^x=\frac{28-26}{18}=\frac19\Rightarrow x=-2$

Нули знаменателя:$x+1=0\Rightarrow x=-1$

Нанесем нули на числовую прямую, расставим знаки, при этом учитываем ОДЗ:

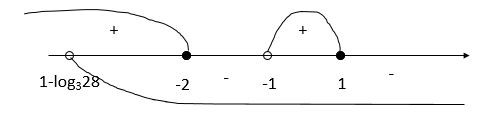
Ответ: (1-log₃28; -2]⋃(-1; 1]