Задание № 21698
Решите неравенство 93+log3x⋅log39x≤log23x−log3x227.
Решать другие задания по теме: Неравенства
Показать ответ
Комментарий:
ОДЗ: x>0
93+log3x(2−log3x)≤(log3x)2−2log3x+3
93−(log3x)2+2log3x≤(log3x)2−2log3x+3
−9−((log3x)2−2log3x+3)((log3x)2+2log3x−3)(log3x)2+2log3x−3≤0
−9−(((log3x)2+2log3x)2−9)(log3x)2+2log3x−3≤0
−(log3x)4+4(log3x)3−4(log3x)2(log3x)2+2log3x−3≤0
(log3x)2((log3x)2−4log3x+4)(log3x)2+2log3x−3≥0
(log3x)2(log3x−2)2(log3x)2+2log3x−3≥0
Нули числителя: log3x=0
x=1 - корень кратности 2
(log3x−2)=0
log3x=2
x=9 - корень кратности 2
Нули знаменателя: log3x=−1 x=13
log3x=3 x=27
Нанесем нули на числовую прямую и, учитывая ОДЗ, определим знаки и промежутки:
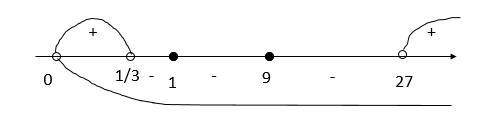
Ответ: (0;13)∪{1;9}∪(27;+∞)
Ответ:Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.