Задание № 21696
Дано уравнение (25sinx)cos2x=5sin(π−x).
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [−5π4;−π4].
Решать другие задания по теме: Уравнения
Показать ответ
Комментарий:
А) Преобразуем уравнение:
(25sinx)cos2x=5sin(π−x)
(25sinx)1−2sin2x=5sinx
52(sinx−2sin3x)=5sinx
снования равны, значит и показатели равны
2(sinx−2sin3x)=sinx
sinx(1−4sin2x)=0
sinx=0
x=πn, n∈Z
1−4sin2x=0
1−4(1−cos2x)=0
cos2x=34
cosx=±√32
x=±π6+πn
Б) Нанесем корни на числовую прямую и определим попадание в отрезок:
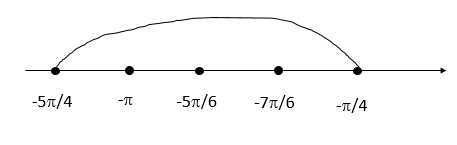
Ответ: А) ±π6+πn,πk;n,k∈Z
Б) −π;−5π6;−7π6
Ответ:Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.