Задание № 21682
Найдите все значения параметра а, при каждом из которых уравнение log22|4−x2|−2a⋅log2|x2−4|+a+6=0 имеет ровно четыре различных корня.
(log2|x2−4|)2−2alog2|x2−4|+a+6=0
Перед нами квадратное уравнение относительно log2|x2−4|
Найдем дискриминант D=4a2−4(a+6)=4a2−4a−24
Уравнение не имеет решение, если 4a2−4a−24<0
Нули: a=−2;a=3
Нанесем на числовую прямую и определим знаки:
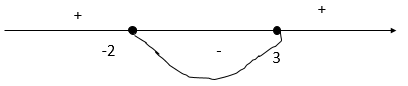
Значит при a∈(−2;3) уравнение не имеет решений.
Рассмотрим случай, когда a∉(−2;3)
Найдем корни: log2|x2−4|=a±√a2−a−6
|x2−4|=2a±√a2−a−6
x2=4±2a±√a2−a−6
Определим количество корней на концах промежутка:
a=−2 x2=54;x2=154 - четыре корня, входит в ответ
a=3;x2=12;x2=−4 - два корня, не входит в ответ
В остальных случаях x2=4±2a±√a2−a−6
Значит, необходимо чтобы два из них не подходили под условие, что x2>0
т.е имеем, что 4−2a±√a2−a−6<0
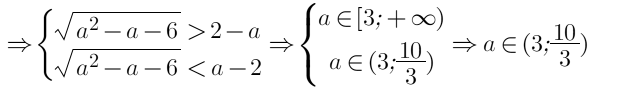
Ответ: {−2}∪(3;103)
Ответ:Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.