Задание № 21663
Найдите все значения параметра а, при каждом из которых уравнение 2sinx+4sinx+√sinx+2=a⋅log2(161+sinx)2sinx+4sinx+√sinx+2=a⋅log2(161+sinx) не имеет корней.
Пусть t=sinxt=sinx, −1≤t≤1−1≤t≤1
2t+4t+√t+2=a⋅log2(161+t)2t+4t+√t+2=a⋅log2(161+t), ОДЗ: t≥0⇒0≤t≤1t≥0⇒0≤t≤1
Рассмотрим на участке t∈[0;1]t∈[0;1]:
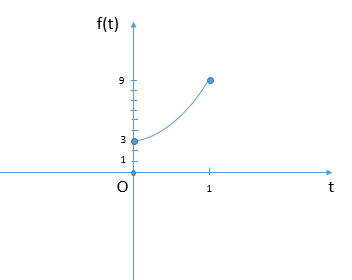
f(t)=2t+4t+√t+2f(t)=2t+4t+√t+2 - монотонно возрастает при t∈[0;1]t∈[0;1]
fmin=f(0)=1+0+0+2=3fmin=f(0)=1+0+0+2=3
fmax=f(1)=2+4+1+2=9fmax=f(1)=2+4+1+2=9
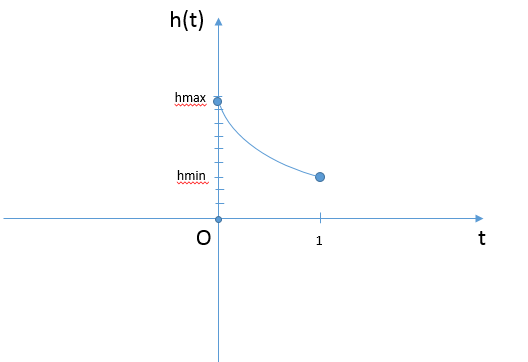
Рассмотрим h(t)=alog2(161+t)h(t)=alog2(161+t) на участке t∈[0;1]t∈[0;1]
При a≥0a≥0 h(t)h(t) неотрицательна при t∈[0;1]t∈[0;1] и монотонно убывающая
Тогда
hmin=h(0)=alog2(161+0)=4ahmin=h(0)=alog2(161+0)=4a
hmax=h(1)=alog2(161+1)=3ahmax=h(1)=alog2(161+1)=3a
При a<0a<0 график h(x) полностью лежит в нижней полуплоскости.
Рассмотрим уравнение при a<0, тогда графическое решение:
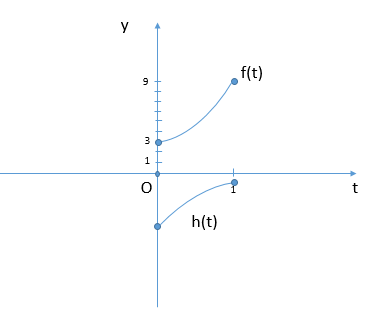
Откуда следует, что при a<0 уравнение не имеет решений!
Рассмотрим уравнение при a≥0, тогда его графическое решение:
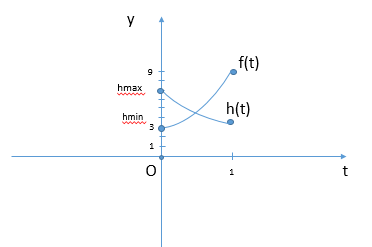
Откуда следует, что
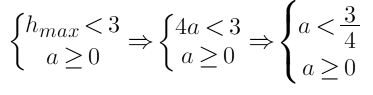
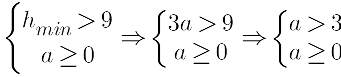
Объединение решений: a∈(−∞;34)∪(3;+∞)
Ответ: (-∞; 0,75)⋃(3; +∞)
Ответ:Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.