Задание № 21470
Конус с высотой 8 см и радиусом основания 6 см разделили на две части осевым сечением. Найдите площадь полной поверхности одной из получившихся фигур. Ответ выразите в см2. Число π следует принять равным 3,14.
Решать другие задания по теме: Задачи по стереометрии
Показать ответ
Комментарий:
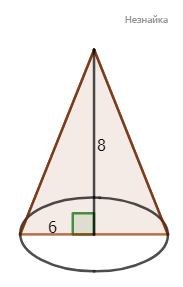

По теореме Пифагора находим образующую l=√(r2+h2)=√(82+62)=10. Площадь поверхности конуса равна Sк=π⋅r⋅l+πr2=3,14⋅6⋅10+3,14⋅62=188,4+113,04=301,44. Если конус рассечь осевым сечением, то площадь поверхности будет равна сумме треугольника и половине изначальной площади S=Sтр+Sк/2=h⋅2r/2+Sк/2=8⋅6+301,44/2=198,72
Ответ: 198,72Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.