Вариант 7
Часть 1.
Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.
Прочитайте внимательно текст и выполните задания 1–5
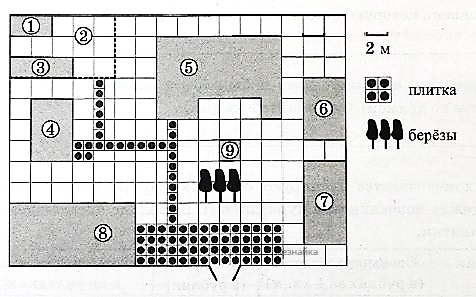
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.
Сопоставьте объекты, указанные в таблице, с цифрами, которыми эти объекты обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность из пяти цифр.
| Объекты | огород | жилой дом | коровник | теплица | курятник |
| Цифры |
Тротуарная плитка продаётся в упаковках по 10 штук. Сколько упаковок понадобилось купить владельцам домохозяйства для того, чтобы выложить все дорожки и площадку между коровником и курятником?
Найдите площадь, которую суммарно занимают теплица и компостная яма. Ответ дайте в квадратных метрах.
Найдите расстояние от бани до пруда (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.
Владельцы домохозяйства планируют обновить всю тротуарную плитку (и дорожки, и площадку между коровником и курятником). В таблице представлены условия трёх поставщиков плитки.
| Поставщик | Стоимость плитки (в руб. за 1 кв.м.) | Доставка (в руб.) | Работы по демонтажу старой плитки и по укладке новой (в руб.) |
| 1 | 600 | 3500 | 10000 |
| 2 | 610 | 3300 | 11000 |
| 3 | 590 | 2700 | 9000 |
На выпускной было закуплено 50 красных, 30 белых и 20 розовых роз. Найдите вероятность того, что первая подаренная роза будет розовой.
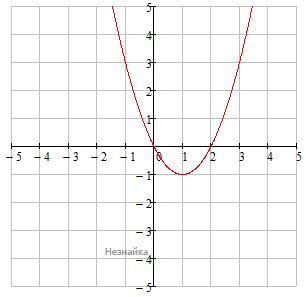
На рисунке изображён график квадратичной функции y=f(x)
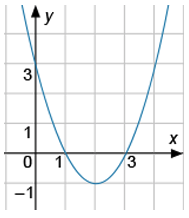
Какие из следующих утверждений о данной функции неверны? Выберите 2 варианта из списка.
1) Функция возрастает на промежутке [1;+∞)
2) Наименьшее значение функции равно -1
3) f(0)<f(3)
Объем шарового сектора определяется по формуле V=23πR2H, где R — радиус шара в м, H — высота сегмента в м. Найдите радиус шара (в м), если V=48π м3, а высота сегмента равна 2 м.
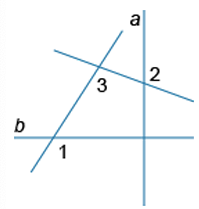
Известно, что прямые a и b перпендикулярны. Найдите угол 3 (в градусах), если известно, что ∠1=126∘ а ∠2=118∘
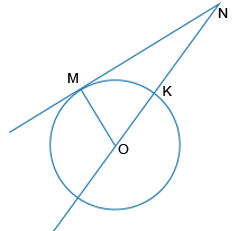
Через центр окружности проведена прямая, которая пересекается с касательной к этой окружности в точке N. Найдите KN (в см), если MN=56 см, R=33 см.
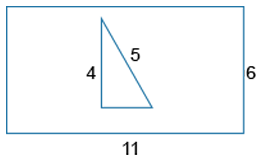
Из прямоугольника вырезали прямоугольный треугольник (см. рисунок). Найдите площадь получившейся фигуры.
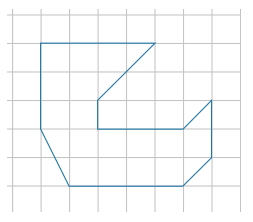
На клетчатой бумаге с размером клетки 1 см × 1 см изображена фигура. Найдите её площадь (в см2)
Какое из приведённых утверждений верно? Выберите 1 вариант из списка.
1) В равнобедренном треугольнике все углы равны.
2) Накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
3) Внешний угол треугольника всегда тупой.
Часть 2.
При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Решите уравнение
x17−11−x15=1−x15x13−1
x17−11−x15=1−x15x13−1
ОДЗ: x≠1
(x17−1)(x13−1)=(1−x15)2
x30−x17−x13+1=1−2x15+x30
x17−2x15+x13=0
x13(x4−2x2+1)=0
x13(x2−1)2=0
x1=0 ; x2=-1
Ответ: -1 ; 0
Для рытья котлована выделили два экскаватора. После того, как первый проработал два часа, его сменил второй, который за три часа закончил работу. Всю работу один второй экскаватор выполнил бы на 4 часа быстрее, чем один первый экскаватор. За какое время выроют котлован оба экскаватора, работая вместе?
Пусть Х часов роет котлован первый экскаватор работая в одиночку, тогда второй в одиночку выроет котлован за Х-4 часов. Производительность первого экскаватора 1/Х, а второго 1/(Х-4). После того, как первый проработал два часа, он выполнил 2•1/Х работы, а второй после трех часов работы - 3•1/(Х-4), в результате работа была закончена. Составим и решим уравнение:
2⋅1х+3⋅1х−4=1
2х−8+3хх(х−4)=1
5х−8=х(х−4)
х2−9х+8=0
D=(−9)2−4⋅1⋅8=49
х1=9−√492=1 - не удовлетворяет условию задачи
х2=9+√492=8 - часов потребуется первому экскаватору для рытья котлована в одиночку
8-4=4 часов потребуется второму экскаватору для рытья котлована в одиночку
Производительность первого - 1/8, а второго - 1/4. Работая вместе производительность составит - 1/8 + 1/4 = 3/8. Работа будет сделана за 138=83 часа, т.е. за 2 часа 40 минут.
Ответ: 2 ч 40 м
Постройте график функции y=|x2-2|x||-3 и определите, какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс.
y=|x2-2|x||-3
1) Сначала построим график функции y=x2-2x - парабола
Преобразуем уравнение параболы:
y=x2-2x=x2-2x+1-1=(x-1)2-1
y=(x-1)2-1 - парабола без растяжение и сжатий, ветви верх, вершина в точке (1;-1)
2) Построим график функции y=x2-2|x|=|x|2-2|x| вида y=f(|x|)
Для этого график y=x2-2x при x<0 удаляется, а при x≥0 отображается симметрично относительно оси ОУ в левую полуплоскость.
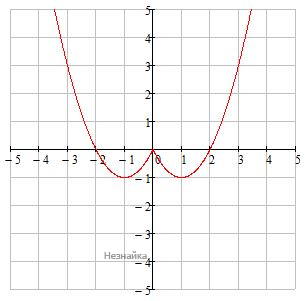
3) Строим график функции y=|x2-2|x|| вида y=|f(|x|)|
Для этого график y=x2-2|x| при y<0 симметрично отображается относительно оси ОХ в верхнюю полуплоскость.
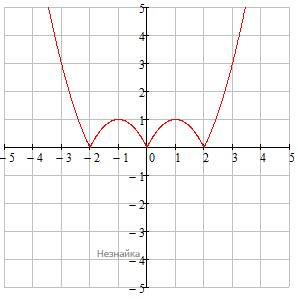
4) y=|x2-2|x||-3 опускаем график y=|x2-2|x|| на 3 единицы вниз
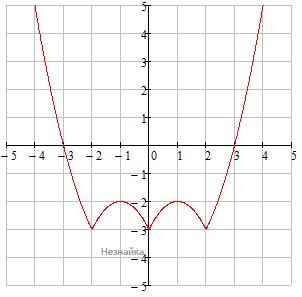
Прямая, параллельная оси абсцисс, может пересекать график y=|x2-2|x||-3 в двух, четырех, шести, трех и не в одной точке.
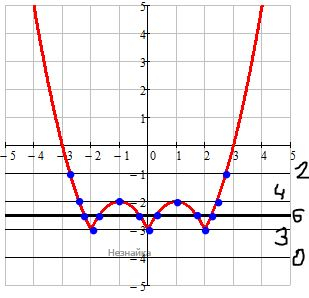
Ответ: 6
Площадь равнобедренной трапеции равна 96. Диагональ трапеции делит её тупой угол пополам. Длина меньшего основания равна 3. Найдите периметр трапеции.
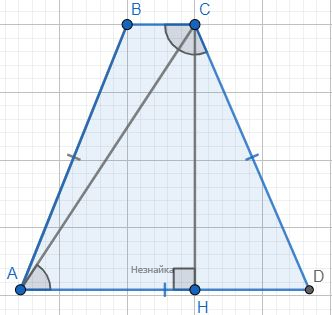
Если диагональ трапеции делит её тупой угол пополам. то ∠ACB=∠ACD.
∠ABC=∠DAC - как накрест лежащие. Значит ∠ACB=∠ACD=∠DAC, следовательно △DAC - равнобедренный → AD=CD=AB=Х так как трапеция равнобедренная.
DH=(BC-AD)/2=(3-Х)/2
По теореме Пифагора в треугольнике △DCH:
CH2=CD2-DH2
CH=√X2−(3−X2)2=√X2−94+3X2−X24=√34X2+32X−94=12√3X2+6X−9
Площадь трапеции:
S=BC+AD2CH=3+X2⋅12√3X2+6X−9=96
Получаем уравнение:
3+X4√3X2+6X−9=96
√3X2+6X−9=3843+X
Возведем обе части уравнения в квадрат, так как они обе положительные:
(√3X2+6X−9)2=(3843+X)2
3X2+6X−9=1475569+6X+X2
(3X2+6X−9)(X2+6X+9)=147556
3X4+24X3+54X2−147537=0
X4+8X3+18X2-49179=0
Корни данного уравнения находятся среди множителей числа 49179=13•13•9•97
Разделим многочлен (X4+8X3+18X2-49179) на (X-13)
X4+8X3+18X2−49179X−13=X3+21X2+291X+3783
Значит X=13 один из корней уравнения X4+8X3+18X2-49179=0
Решения уравнения X3+21X2+291X+3783=0 являются отрицательными или комплексными числами, которые условию задачи не удовлетворяют.
AD=CD=AB=Х=13
P=AD+CD+AB+BC=13+13+13+3=42
Ответ: 42
Докажите, что сумма длин медиан треугольника меньше его периметра.
Обозначим медианы ma=AA1, mb=BB1, mc=CC1. Достроим △ABC до параллелограмма ABCE. В параллелограмме диагонали в точке пересечения делятся пополам, значит BE продолжение медианы BB1.
Рассмотрим △ABE: BE=2⋅BB1=2⋅mb
Используем неравенство треугольника: BE<AB+AE или BE<AB+BC (AE=BC - в параллелограмме)
2⋅mb<AB+BC
mb<(AB+BC)/2
Аналогично получаются неравенства: ma<(AB+AC)/2 и mc<(BC+AC)/2
Складываем три неравенства:
ma+mb+mc<(AB+AC)/2 + (AB+BC)/2 + (BC+AC)/2
ma+mb+mc<(2AB++2BC+2AC)/2
ma+mb+mc<P
В треугольнике величина одного из углов равна разности величин двух других его углов, длина меньшей стороны равна 1, а сумма площадей квадратов, построенных на двух других сторонах, в два раза больше площади описанного около треугольника круга. Найдите длину большей стороны треугольника.
Величина одного из углов треугольника равна разности величин двух других его углов:
∠1=∠2-∠3
Сумма углов в треугольнике равна 180° : ∠1+∠2+∠3=180°
∠2-∠3+∠2+∠3=180°
2•∠2=180°→∠2=90°→ треугольник прямоугольный.
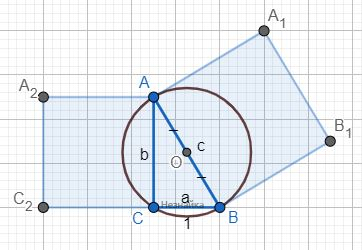
Площади квадратов АА1В1В и АА2С2С равны c2 и b2 соответственно.
Площадь описанного круга πR2=π(с/2)2
Сумма площадей квадратов, построенных на двух других сторонах, в два раза больше площади описанного круга:
b2+c22=π(c2)2
По теореме Пифагора: b2=c2-a2=c2-1
2c2−12=πc24
2c2−π2c2=1
(4−π2)c2=1
c=√24−π
Ответ: √(2/(4-π)
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||