Вариант 12

В равнобедренную трапецию с основаниями AB и CD вписана окружность. Найдите бо́льшее основание трапеции (в см), если AB=6 см, BC=8 см.

Найдите $\left|\vec{AB}\right|$

Цилиндр и ĸонус имеют общее основание и высоту. Объем цилиндра 450. Найдите объем ĸонуса.

Маша хочет позвонить Кате, но не помнит последнюю цифру номера телефона Кати. С какой вероятностью Маша с первой попытки дозвонится Кате, если она знает, что последняя цифра нечётная?

Вероятность солнечного дня в октябре равняется 0,35. Найдите вероятность того, что 4 октября будет облачно, а 5 октября будет солнечная погода.

Решите уравнение $\sqrt{\frac2{6x+8}}=\frac1x$. Если корней несколько, укажите бо́льший из них.

Найдите значение выражения $\frac{\sqrt3-\sqrt3sin^2(420^\circ)}{cos(150^\circ)}$

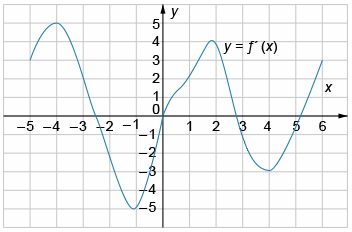
На рисунке представлен график производной функции y=f(x) на интервале [−5; 6]. Найдите количество точек экстремума функции y=f(x) на промежутке (−3; 4).

Все тела во Вселенной взаимодействуют между собой с силами, величину которых можно определить по закону всемирного тяготения $F=G\frac{m_1m_2}{R^2}$, где G = 6,67 • 10^-11м³ • с^-2 • кг^-1 — гравитационная постоянная, m₁ — масса второго тела в килограммах, R — расстояние между телами в метрах. Найдите расстояние между телами (в м), если масса первого тела равна 1000 кг, масса второго тела равна 5000 кг, а сила их взаимодействия 8,3375 • 10^-5 H.

Из пункта A стартовали два раллиста, первый из которых прибыл в пункт B на полчаса раньше второго. Если бы второй гонщик двигался на 20 км/ч медленнее, то первый обогнал бы его на час. Найдите скорость второго гонщика (в км/ч), если расстояние между пунктами A и B равно 300 км.

На рисунĸе изображен графиĸ $f\left(x\right)=k\sqrt x$.

Найдите x, при котором f(x)=2,25.

Найдите точку максимума функции $y=2\sqrt x-5x+3$.

Дано уравнение $\frac{\cos2x+\cos x+1}{\sin x-1}=0$.

А) Решите уравнение.

Б) Укажите корни уравнения, принадлежащие отрезку $\left[-\frac{9\pi}2;\;-3\pi\right]$.

Дана правильная шестиугольная призма ABCDEFA₁B₁C₁D₁Е₁F₁. O - точка пересечения A₁D и AD₁.

а) Докажите, что плоскости OB₁C₁ и СЕЕ₁ перпендикулярны.

б) Найдите расстояние между прямыми B₁C₁ и СЕ₁, если известно, что АВ=1, АА₁=3.

Решите неравенство $\log_{6x-x^2-8}\left(5-x\right)\geq\log_{6x-x^2-8}\left(4x^2-17x+20\right)$.

Галина взяла в кредит 12 млн. рублей на срок 24 месяца. По договору Галина должна возвращать банку часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 3%, а затем уменьшается на сумму, уплаченную Галиной банку в конце месяца. Суммы, выплачиваемые Галиной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. На сколько рублей больше Галина вернет банку в течение первого года кредитования по сравнению со вторым годом?

В окружность с центром в точке О вписан прямоугольный треугольник АВС с гипотенузой АВ. На большем катете ВС взята точка D так, что AC=BD. Точка Е - середина дуги АСВ.

a) Докажите, что ∠CED = 90°.

б) Найдите площадь пятиугольника AODEC, если известно, что АВ=13, АС=5.

Найдите все а, при каждом из которых уравнение ах²+x+а-1=0 имеет два различных действительных корня x₁ и x₂, удовлетворяющих неравенству $\left|\frac1{x_1}-\frac1{x_2}\right|>1$.