Вариант 7
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
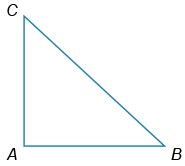
В прямоугольном треугольнике ABC угол A равен 90°. Найдите сторону AC (в см), если tg∠C=74, CB=2√65 см.
Дано 2 ĸонуса. Радиус первого ĸонуса в 2 раза больше радиуса второго. А образующая в 3 раза меньше. Во сĸольĸо раз площадь боĸовой поверхности 1 ĸонуса больше площади второго.
На производстве при упаковке чая вероятность того, что упаковка окажется не герметичной, равна 0,09. Найдите вероятность того, что две произвольно выбранные упаковки чая окажутся герметичными.
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Геолог» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Геолог» выиграет жребий ровно два раза.
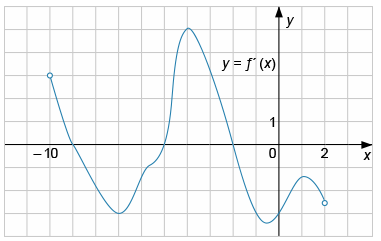
На рисунке представлен график производной функции y=f '(x) на интервале (−10; 2). Найдите точку минимума функции y=f(x) на данном промежутке.
Координата тела при равноускоренном движении изменяется по закону x=x0+v0t+at22, где x0 — начальная координата тела, a — ускорение тела, t — время движения тела. Найдите время движения тела, если его ускорение равно 2 м/c2, начальная координата равна 7 м, а координата в конце движения равна 67 м при начальной скорости 11 м/с.
Из одного порта в другой по течению выплыл плот, через два часа ему навстречу выплыла моторная лодка, они встретились через 4 часа после отправления лодки. Найдите скорость лодки (в км/ч), если скорость течения равна 3 км/ч, а расстояние между портами равно 146 км.
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите наименьшее значение функции y=4x+1x+7 на промежутке (0;2)
f′(x)=4−1x2
4−1x2=0
x=±12, но заданному промежутку удовлетворяет толькоx=12
x=12 - критическая точка
f(12)=2+2+7=11
maxf(x)=11 на заданном промежутке
Дано уравнение 4cos4x - 5cos2x - 1 = 0.
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [arccos0; arccos(-1)].
А) Преобразуем уравнение:
4(1+cos2x2)2−5cos2x−1=0
1+2cos2x+cos22x−5cos2x−1=0
cos22x−3cos2x=0
cos2x(cos2x−3)=0
т.е. имеем, что cos2x=0 или cos2x−3=0
В первом случае 2x=π2+πn; x=π4+πn2, n∈Z
Во втором случае ∅, так как не соответствует области значений косинуса
Б) Нанесем корни на числовую прямую и определим, какие корни входят в отрезок:
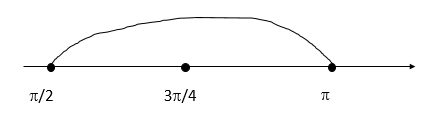
Ответ:
А) π4+πk2;k∈Z;
Б) 3π4
Цилиндр и конус имеют общее основание, вершина конуса является центром другого основания цилиндра. Каждая образующая конуса наклонена к плоскости основания под углом 30°.
А) Докажите, что площади боковых поверхностей цилиндра и конуса равны.
Б) Найдите радиус сферы, касающейся боковых поверхностей цилиндра и конуса, а также одного из оснований цилиндра, если известно, что объем конуса равен (6√3+10)⋅π.
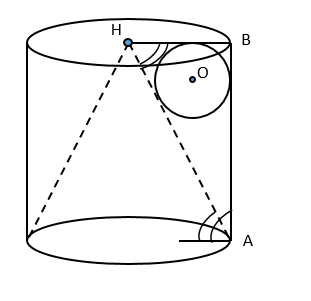
А) Sб.к.=Sб.ц. - доказать
Sб.к.=πr⋅AH ; Sб.ц.=2πr⋅AB
Рассмотрим △ABH, H - центр основания цилиндра, BA⊥ нижнему основанию цилиндра, ∠B=90∘
sin(∠H)=ABAH=sin(30∘)=12⇒AB=12AH
⇒Sб.ц.=2πr⋅12AH=πr⋅AH=Sб.к., что и требовалось доказать
Б) Vк=(6√3+10)π, r0 - ?
т. О - центр сферы, пусть т. O∈(ABH)
⇒r0= радиусу вписанное в △ABH окружности
⇒r0=HB+AB−AH2=R+h−hsin(∠H)2=R−h2
hR=tg(∠H)⇒h=R⋅tg(30∘)=R√33
Vк=13πR2h=13πR2⋅R√33=πR3√39, r0=R(1−√33)2⇒R=2r01−√33
⇒π√39⋅(2r01−√33)3=(6√3+10)π
8√39r30=12√3−20+20−100√39
r30=1
r0=1
Ответ: 1
Решите неравенство log3√28⋅3x−3x+1≥1.
Перенесем единицу в левую часть и приведем к общему знаменателю:
log3√28⋅3x−3−(x+1)x+1≥0
ОДЗ: 28⋅3x−3>0
x>log3328
x>1−log328
Нули числителя: 12log3(28⋅3x−3)−(x+1)=0
log3(28⋅3x−3)=2(x+1)
28⋅3x−3=32(x+1)
9⋅32x−28⋅3x+3=0
D=646
3x=28+2618=3⇒x=1
3x=28−2618=19⇒x=−2
Нули знаменателя:x+1=0⇒x=−1
Нанесем нули на числовую прямую, расставим знаки, при этом учитываем ОДЗ:
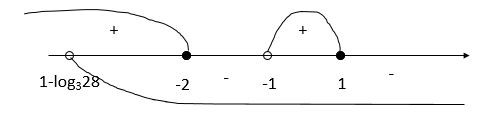
Ответ: (1-log328; -2]⋃(-1; 1]
16 ноября близнецы Саша и Паша взяли в банке кредит по 500 тысяч руб. каждый сроком на четыре месяца. Условия возврата кредита таковы:
• 28-го числа каждого месяца долг увеличивается на 10 % по сравнению с 16-м числом текущего месяца;
• с 1-го по 15-е число каждого месяца необходимо выплатить часть долга; 16-го числа каждого месяца долг должен составлять некоторую сумму в соответствии с предложенной для каждого из них таблицей:
Саша
| Дата | 16.11 | 16.12 | 16.01 | 16.02 | 16.03 |
| Долг, тыс. руб. | 500 | 300 | 200 | 100 | 0 |
Паша
| Дата | 16.11 | 16.12 | 16.01 | 16.02 | 16.03 |
| Долг, тыс. руб. | 500 | 400 | 300 | 200 | 0 |
Kто из братьев за четыре месяца выплатит банку меньшую сумму? На сколько рублей?
Решение:
Составим таблицу выплат каждого из близнецов и посчитаем итоговую сумму выплаты по каждому:
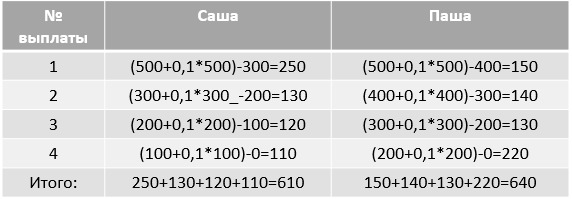
Получим, что Саша выплатит меньше на 30 тыс. ( 640-610=30)
Ответ: Саша выплатит меньше на 30 тыс.
В прямоугольном треугольнике АВС известно, что ВС=2⋅АС. На гипотенузе АВ вне треугольника построен квадрат ABEF. Прямая СЕ пересекает АВ в точке О.
А) Докажите, что ОА:ОВ=3:4.
Б) Найдите отношение площадей треугольников АОС и ВОЕ.
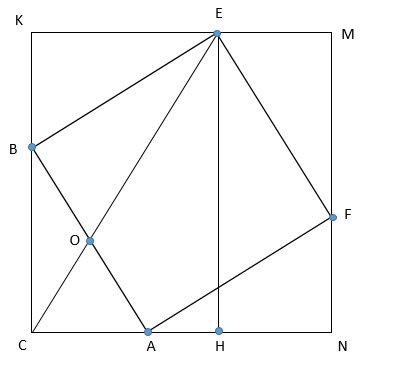
А) Достроим до квадрата CKMN так, чтобы △ABC=△FAN=△EFM=△BEK
Обозначим ∠OCA=α и запишем теорему синусов для △OCA и △OCB:
OCsin(∠OBC)=OBsinn(90∘−α)
⇒OAOB⋅cosαsinα=sin(∠OBC)sin(∠OAC)
⇒OAOB=sin(∠OBC)sin(∠OAC)⋅tgα
Опустим из Е перпендикуляр на CN. EH⊥CN;EH=MN=CA+BC=3AC
HN=EM (по свойству прямоугольника EMNH)
⇒CH=CN−HN=3AC−AC=2AC
⇒tg(∠ECH)=tgα=32
Рассмотрим △ABC: по теореме Пифагора AB=√AC2+BC2=√AC2+4AC2=√5AC
sin(∠ABC)=sin(∠OBC)=AC√5AC=1√5
sin(∠BAC)=sin(∠OAC)=2AC√5AC=2√5
⇒OAOB=1√5⋅√52⋅32=34, ч.т.д.
Б) S△AOCS△BOE−?
S△AOC=12AO⋅AC⋅sin(∠AOC)=12⋅37AB⋅AC⋅2√5=37√5AC⋅√5⋅AC=37AC2
S△BOE=12BO⋅BE=12⋅47⋅AB⋅AB=27⋅(AC√5)2=107AC2
⇒S△AOCS△BOE=37AC2107AC2=310
Ответ: 0,3
Найдите все а, при каждом из которых в область значений функции y=8x−a−68x2+8 входит ровно два целых числа. Для каждого такого а укажите эти целые числа.
Решение: так как нам дана дробь, и числитель является линейной функцией , то какое бы a мы не взяла всегда найдется значение х, в котором числитель равен 0, соответственно и исходная функция. ( такой же вывод можно сделать из предела функции)
Исходная функция непрерывна на x∈R. Требуется по условию, что в область значений входит только два целых числа, значит имеем два варианта: 0 и 1, 0 и -1. Рассмотрим два случая.
1 сл: 0 и 1
Решим уравнение:
8x−a−68x2+8=1
8x2−8x+a+14=0
D=64−32(a+14)≥0
a≤−12
Учтем, что значения функции в данном случае лежит в пределах (−1;2) при x∈R
Решим неравенство −1<8x−a−68x2+8<2.
Решение: a>−21;a<0. Получим, учитывая область значений функции, что a∈(−21;−12]
2 сл: 0 и -1
Решим уравнение:
8x−a−68x2+8=−1
8x2+8x−a+2=0
D=64−32(−a+2)≥0
a≥0
Учтем, что значения функции в данном случае лежит в пределах (−2;1) при x∈R
Решим неравенство −2<8x−a−68x2+8<1.
Решение: a>−12;a<9. Получим, учитывая область значений функции, что a∈[0;9)
Ответ: a∈(-21; -12]⋃[0; 9);
при а∈(-21; -12] y=0 и y=1;
при а∈[0; 9) y=0 и y=-1
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||