Вариант 2

Сначала найдем производную функции и точки, в которых она равна 0 или не существует:

f'(x)=(3x²—13,5x²—36x+10,6)'=9x²—27x—36

f'(x)=0, при x₁=—1, x₂=4

При x<—1 — производная положительная — функция возрастает, при —1<x<4 — производная отрицательная — функция убывает, при x>4 — производная положительная — функция возрастает. Значит x=—1 точка максимума

A) Пусть $sinx+cosx=t$ . Тогда $t^2=sin^2x+2sinx\cdot cosx+cos^2x$

$t^2-2sinx\cdot cosx=1$

Получаем:

$t^2-1=3(t-1)$

$t^2-3t+2=0$

Решим уравнение и получим: $t_1=1$ ,$t_2=2$

Выполним обратную подстановку:

$sinx+cosx=1$

$\sqrt2(\frac{\sqrt2}2sinx+\frac{\sqrt2}2cosx)=1$

$(cos\frac\pi4sinx+sin\frac\pi4cosx)=\frac1{\sqrt2}$

$sin(\frac\pi4+x)=\frac{\sqrt2}2$

$\frac\pi4+x=\left(-1\right)^n\frac\pi4+2\pi n$ $;n\in Z$

$2\pi k,\;k\in Z;\;\frac\pi2+2\pi n,\;n\in Z$

Б) Нанесем корни на числовую прямую:

В нужный нам промежуток входит только один корень $\frac\pi2$

Ответ:А) $2\pi k,\;k\in Z;\;\frac\pi2+2\pi n,\;n\in Z$

Б) $\frac\pi2$

Решение:

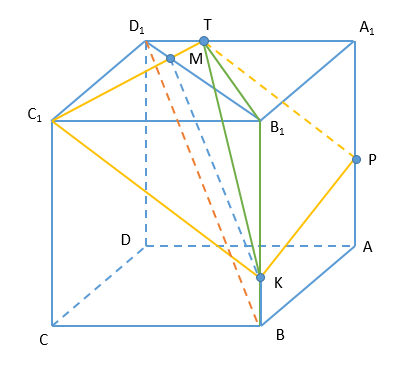
А) 1. Проведем $KM\vert\vert BD_1$, $M\in(BB_1D_1)$ , $M\in(A_1B_1C_1)$

Проведем $CM\cap A_1D_1=T$

$(BB_1C)\vert\vert(ADD_1)\Rightarrow T\in AA_1$ $TP\vert\vert KC_1$

Имеем, что $(PTK)$-плоскость, $PTC_1K$-сечение параллелепипеда плоскостью $\alpha$

2. $\bigtriangleup B_1MK$ и $\bigtriangleup B_1D_1B$ - подобны ($\angle B_1$-j,общий, $KM\vert\vert BD_1\Rightarrow\angle B_1MK=\angle B_1D_1B$)$\Rightarrow$ $\frac{D_1M}{MB_1}=\frac{BK}{KB_1}=\frac14$

$\bigtriangleup C_1MB_1\sim\bigtriangleup TMD_1$ (все углы попарно равны)$\Rightarrow$$\frac{D_1T}{B_1C_1}=\frac{D_1M}{MB_1}=\frac14$

$\frac{A_1T}{B_1C_1}=\frac34$

$\bigtriangleup PA_1T\sim\bigtriangleup KB_1C_1$ $\Rightarrow$ $\frac{A_1P}{B_1K}=\frac{A_1T}{B_1C_1}=\frac34$

Получим, что $A_1P=\frac35BB_1$. Тогда $AP=\frac25BB_1$

$\frac{AP}{AP_1}=\frac23$, чтд

Б) $(TB_1K)$ делит пирамиду $B_1TC_1KP$на две пирамиды. Найдем их объем:

$V_{B_1TC_1K}=\frac13\cdot S_{B_1C_1K}\cdot С_1D_1=\frac13\cdot\frac12\cdot4\cdot4\cdot3=8$

$V_{B_1TPK}=\frac13\cdot S_{B_1PK}\cdot A_1T=\frac13\cdot\frac12\cdot4\cdot3\cdot3=6$

$V_{B_1TPKC_1}=8+6=14$

Ответ: 14

ОДЗ: $x>0$, $x\neq1$, $3x-1>0$

Преобразуем левую часть неравенства:

$log_x(3x-1)(log_x(3x-1)-1)\geq0$

$\frac{ln(3x-1)}{lnx}(\frac{ln(3x-1)-lnx}{lnx})\geq0$

$\frac{ln(3x-1)}{ln^2x}(\frac{ln(3x-1)-lnx}1)\geq0$

Нули числителя: $ln(3x-1)=0$

$3x-1=1$

$x=\frac23$

$ln(3x-1)=lnx$

$3x-1=x$

$2x=1$

$x=\frac12$

Нули знаменателя:

$lnx=0$

$x=1$ - корень кратности 2

Нанесем корни на числовую прямую, учитываю ОДЗ:

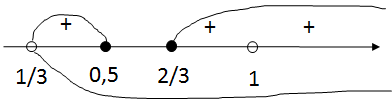
Получаем следующие промежутки: $(\frac13;\;\frac12\rbrack\cup\lbrack\frac23;\;1)\cup\left(1;\;+\infty\right)$

Ответ: $(\frac13;\;\frac12\rbrack\cup\lbrack\frac23;\;1)\cup\left(1;\;+\infty\right)$

Пусть $x$л - количество глицерина в сосуде изначально. После первого переливания получим глицерина $(x-1)$л. т.е доля глицерина в сосуде равна $\frac{x-1}x$. После второго переливания доля глицерина в сосуде составила $\frac{\frac{x-1}x}{\frac{x-1}1}=\left(\frac{x-1}x\right)^2$

Аналогично после третьего переливания: $\frac{\frac{x-1}x}{\left(\frac{x-1}1\right)^2}=\left(\frac{x-1}x\right)^3$

По условию задачи воды в сосуде стало в 7 раз больше, чем глицерина,т.е глицерина в сосуде составило 1 долю, а вода – 7 долей, т.е глицерина в сосуде 1/8

Получаем следующее уравнение:

$\left(\frac{x-1}x\right)^3=\frac18$

$\frac{x-1}x=\frac12$

$x=2$

Таким образом, объем сосуда( первоначальное количество глицерина в сосуде)-2л

Количество глицерина в частях после второго переливания: $\left(\frac{2-1}2\right)^2=\frac14$, а воды- $1-\frac14=\frac34$

Ответ: 2 л; 1:3

Решение:

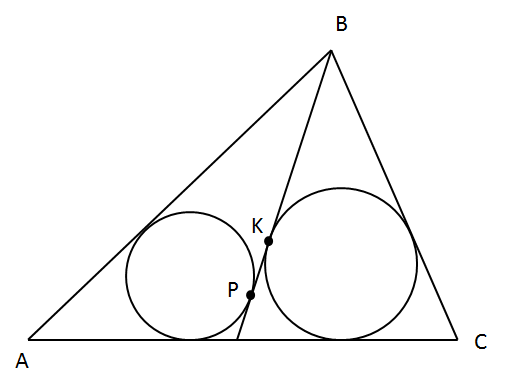
А)Найдем радиус вписанной окружности через следующую формулу: $S=pr$, где $p=\\frac P2$

Отсюда $r=\\frac{2S}P$

Радиус вписанной окружности в треугольник ABM: $r_{ABM}=\\frac{2S_{ABM}}{AB+BM+AM}$

Радиус вписанной окружности в треугольник ABC: $r_{ABC}=\\frac{2S_{ABC}}{AB+BC+AC}$

Пусть $r_{ABM}=\\frac12r_{ABC}$. Тогда

$\\frac{2S_{ABM}}{AB+BM+AM}=\\frac{2S_{ABC}}{AB+BC+AC}$

$S_{ABC}=2S_{ABM}$ , т.к. BM-медиана

Следовательно, знаменатели равны, т.е $BM+AM=BC+2AM$$BC+AM=BM$

Б) Исходя из свойства о том,что прямые, выходящие из одной точки и касающиеся окружности, образуют два равных по величине отрезка, получим следующие выражения $MP=p_{ABM}-AB=\\frac{BM+AM}2-8.5=\\frac{BM+MC}2-8.5$

$MК=p_{СBM}-BC=\\frac{BM+CM}2-3.5$

Получим, что $PK=MK-MP=-3.5+8=5$

Ответ: А) нет; Б) 5

Решение:

ОДЗ:

x-1>0 → x>1

x-1≠1 → x≠2

4^x-1-3⋅2^x-a>0

Введем замену 2^x=t , тогда

1/4t²-3⋅t-a>0

Нули: t₁=6-2√(9+а) , t₂=6+2√(9+а)

t<6-2√(9+а) или t>6+2√(9+а)

1/4t²-3⋅t-a - парабола, ветви которой направленны вверх, так что неравенство 1/4t²-3⋅t-a>0 будет верным и при 9+а<0. Значит, согласно данному условию, a - любое.

x>1 → t>2

x≠2 → t≠4

Преобразуем неравенство: |x - 2|≤ 1

$-1\leq x-2\leq1$

$1\leq x\leq3$

$2\leq t\leq8$

Итого: t≠4, 2<t⩽8

Преобразуем: $\log_{x-1}\left(4^{x-1}-3\cdot2^x-a\right)=0$

$\frac14t^2-3t-a=1$

График функции $\frac14t^2-3t-a-1=y(t)$ имеет экстремум в точке t=6 и нули в точках t₁=6-2√(10+а) , t₂=6+2√(10+а).

1) При t₁=t₂=6 - уравнение имеет одно решение в точке касания графика и оси ОХ: а=-10

2) При 2<t⩽8

Корни t₁=6-2√(10+а)>2 расположены слева от экстремума t=6, при этом корни, расположенные справа от экстремума, должны выходить из промежутка t₂=6+2√(10+а)⩾8. Так будет обеспечено наличие одного корня, удовлетворяющего неравенству |x - 2|≤ 1

6-2√(10+а) > 2

а < -6

6+2√(10+а) ⩾ 8

a ⩾ -9

При a=9 имеем два корня t₂=8 и t₁=4, последний не удовлетворяет ОДЗ, поэтому a=9 удовлетворяет условию о наличии одного корня.

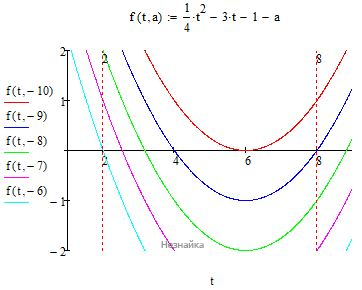
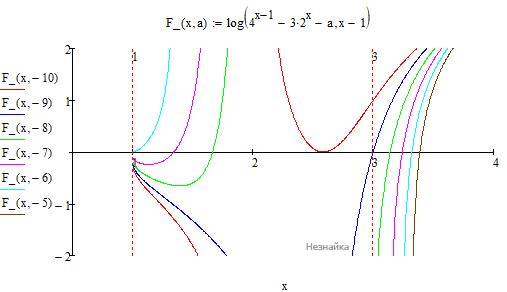
Ответ: $a=-10,\;-9\leq a<-6$