Задание № 7595
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч (по своему выбору) один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 10 камней, а в другой 7 камней; такую позицию в игре будем обозначать (10, 7). Тогда за один ход можно получить любую из четырёх позиций: (11, 7), (20, 7), (10, 8), (10, 14). Для того чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 73. Победителем считается игрок, сделавший последний ход, т.е. первым получивший такую позицию, что в кучах всего будет 73 камня или больше.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока – значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника. Например, при начальных позициях (6, 34), (7, 33), (9, 32) выигрышная стратегия есть у Пети. Чтобы выиграть, ему достаточно удвоить количество камней во второй куче.
Задание 1.
Для каждой из начальных позиций (6, 33), (8, 32) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 2.
Для каждой из начальных позиций (6, 32), (7, 32), (8, 31) укажите, кто из игроков имеет выигрышную стратегию. В каждом случае опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии.
Задание 3.
Для начальной позиции (7, 31) укажите, кто из игроков имеет выигрышную стратегию. Опишите выигрышную стратегию; объясните, почему эта стратегия ведёт к выигрышу, и укажите, какое наибольшее количество ходов может потребоваться победителю для выигрыша при этой стратегии. Постройте дерево всех партий, возможных при указанной Вами выигрышной стратегии. Представьте дерево в виде рисунка или таблицы.
Содержание верного ответа
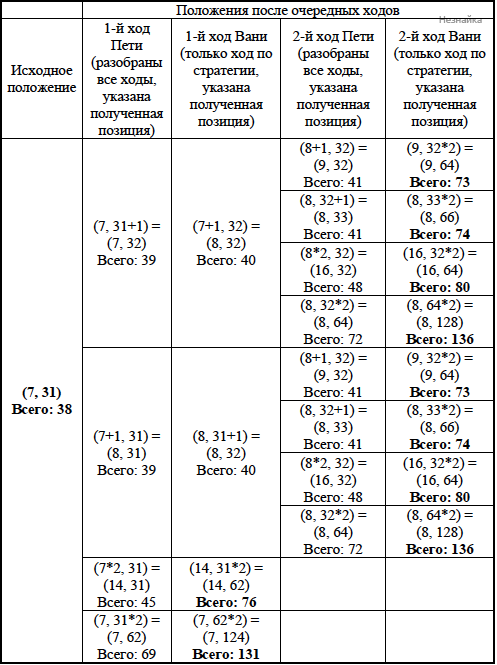
Примечание для эксперта. Дерево всех партий может быть также изображено в виде ориентированного графа – так, как показано на рисунке, или другим способом. Например, вершины дерева, соответствующие одной и той же позиции, на рисунке могут быть «склеены». Важно, чтобы множество полных путей в графе находилось во взаимно однозначном соответствии с множеством партий, возможных при описанной в решении стратегии.
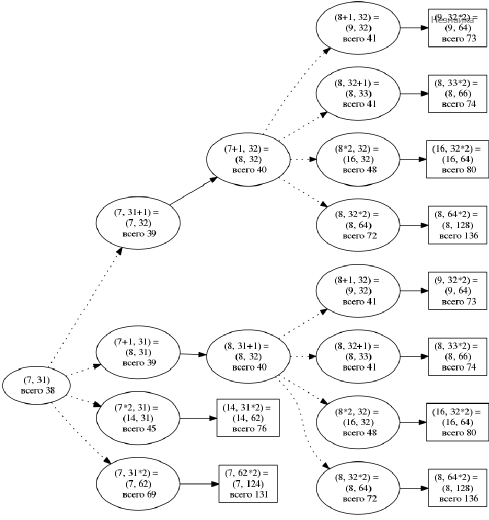
Дерево всех партий, возможных при описанной стратегии Вани. Ходы Пети показаны пунктирными стрелками, ходы Вани показаны сплошными стрелками. Заключительные позиции обозначены прямоугольником.
Примечание для эксперта. В некоторых позициях у Вани есть и другой способ выигрыша: например, в позиции (8, 64) можно добавить один камень в любую кучу. То, что это не указано, не является ошибкой. Экзаменуемый не должен указывать все возможные выигрышные стратегии.
Ответ:Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.