Задание № 7568
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в кучу один, три или двадцать камней. Например, имея кучу из 12 камней, за один ход можно получить кучу из 13, 15 или 32 камней. У каждого игрока, чтобы делать ходы, есть неограниченное количество камней.
Игра завершается в тот момент, когда количество камней в куче становится не менее 35.
Победителем считается игрок, сделавший последний ход, то есть первым получивший кучу, в которой будет 35 или больше камней.
В начальный момент в куче было S камней, 1 ≤ S ≤ 34.
Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Описать стратегию игрока — значит описать, какой ход он должен сделать в любой ситуации, которая ему может встретиться при различной игре противника.
Выполните следующие задания. Во всех случаях обосновывайте свой ответ.
Задание 1
а) Укажите все такие значения числа S, при которых Петя может выиграть в один ход. Обоснуйте, что найдены все нужные значения S, и укажите выигрывающий ход для каждого указанного значения S.
б) Укажите такое значение S, при котором Петя не может выиграть за один ход, но при любом ходе Пети Ваня может выиграть своим первым ходом. Опишите выигрышную стратегию Вани.
Задание 2
Укажите два таких значения S, при которых у Пети есть выигрышная стратегия, причём (а) Петя не может выиграть за один ход и (б) Петя может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Для каждого указанного значения S опишите выигрышную стратегию Пети.
Задание 3
Укажите значение S, при котором:
— у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и
— у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Для указанного значения S опишите выигрышную стратегию Вани. Постройте дерево всех партий, возможных при этой выигрышной стратегии Вани (в виде рисунка или таблицы). На рисунке на рёбрах дерева указывайте, кто делает ход; в узлах — количество камней в куче.
Содержание верного ответа
Задание 1.
а) Петя может выиграть в один ход, если S = 15, ... 34. Во всех этих случаях достаточно добавить 20 камней, после чего их количество станет больше 34, и игра закончится.
При значениях S, меньших 15, за один ход нельзя получить кучу, количество камней в которой будет не менее 35.
б) Ваня может выиграть первым ходом (при любой игре Пети), если S = 14. Тогда после первого хода Пети в куче будет 15, 17 или 34 камня. После этого Ваня добавляет 20 камней и выигрывает в один ход.
Задание 2.
При S = 11 или S = 13 у Пети есть выигрышная стратегия, позволяющая ему выиграть своим вторым ходом. В этих случаях Петя не может выиграть первым ходом (см. п. 1а)). Однако он может получить кучу из 14 камней, добавив в кучу один камень (при S = 13) или три камня (при S = 11). После этого хода Петя попадает в ситуацию, разобранную в п. 16) для Вани, то есть у игрока, делающего следующий ход (у Вани), нет хода, сразу приводящего его к выигрышу, а у Пети выигрышный ход «добавить 20 камней» есть независимо от того, какой ход сделал Ваня.
Задание 3.
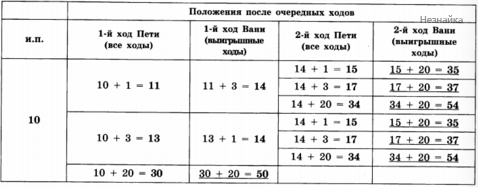
При S = 10 у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом. После первого хода Пети в куче будет 11, 13 или 30 камней. Если в куче станет 30 камней, то Ваня добавит 20 камней и выиграет своим первым ходом. Если после первого хода Пети в куче оказалось 11 или 13 камней, то Ваня попадает в ситуацию, разобранную в п. 2 для Пети, и у него есть выигрышная стратегия, позволяющая ему выиграть своим вторым ходом.
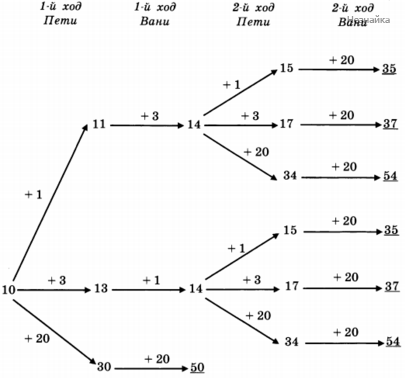
В таблице представлено дерево возможных партий при описанной выигрышной стратегии Вани. На рисунке это же дерево изображено в графическом виде. Заключительные позиции, в которых выигрывает Ваня, подчёркнуты. Приведены все возможные ходы Пети и ходы, отвечающие выигрышной стратегии Вани.
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.