Задание № 23315
На карту нанесены 4 города (А, В, С и D).
Известно, что:
между городами А и С — три дороги, между городами С и В — две дороги, между городами А и В — две дороги, между городами С и D — две дороги, между городами В и D — четыре дороги.
По каждой из этих дорог можно ехать в обе стороны. Сколькими различными способами можно проехать из А в D, посещая каждый город не более одного раза?
[topic]
Рисуем граф, на котором отмечаем все города и пути между ними, начинаем подсчитывать их количество, помня, что через каждый город посещать не более одного раза
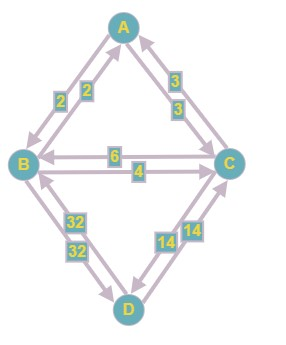
Между A и C три дороги, между A и B -две. Из B в C можно попасть по 2 дорогам, т.е. по пути A=>B=>C будет 2*2=4 пути, а по пути A=>C=>B 3*2=6 путей
Т.е. в C ведут как из А 3 пути, так и через B 4 пути.3+4=7
В город B по той же механике 6+2=8 путей
В D можно попасть из C по двум дорогам и из B по четырем, получаем 7*2+8*4=14+32=46 путей из А в D
Ответ: 46Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.