Произведём присвоение для упрощения. Пусть, (x ∈ A)=А, (x ∈ P)=Р, (x ∈ Q)=Q. После подстановки получается логическое уравнение

После преобразования по формуле:

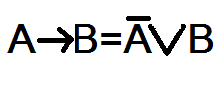
получаем

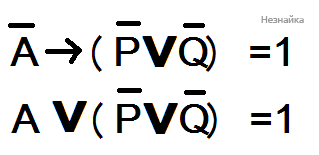
(после второго преобразования отрицание над А убирается т.к. происходит двойное отрицание (Первое давалось изначально второе получили после преобразования) )

В этом логическом уравнении присутствует только логическое сложение следовательно уравнение является истиной когда P или Q раны 0 (не забываем что у нас над P и Q стоит отрицание т.е. при P=0 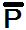=1

Теперь построим прямую

Так как я хочу спать не буду разбирать все отрезки и сразу скажу что ответ 20 (если я не ошибаюсь). Теперь разберёмся почему. 20 это минимальное расстояние между 2-мя заданными точками, а именно расстояние от 30 до 50, которое удовлетворяет уравнению. Вы спросите почему ответ не 10 (от 20 до 30)? Ответ прост. Если мы возьмём точку 35 при отрезке от 20 до 30 то получим что переменная А=0, P=0 (учитывая отрицание), Q=0 (учитывая отрицание)