Рентгеновские лучи были открыты в 1895 г. немецким физиком Вильгельмом Рентгеном. Рентген заметил, что при торможении быстрых электронов на любых препятствиях возникает сильно проникающее излучение, которое учёный назвал X-лучами (в дальнейшем за ними утвердится термин «рентгеновские лучи»). Когда Рентген держал руку между трубкой и экраном, то на экране были видны тёмные тени костей на фоне более светлых очертаний всей кисти руки.

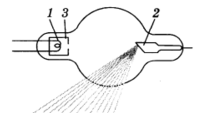
Схема современной рентгеновской трубки для получения X-лучей представлена на рисунке. Катод 1 представляет собой подогреваемую вольфрамовую спираль, испускающую электроны. Поток электронов фокусируется с помощью цилиндра 3, а затем соударяется с металлическим электродом (анодом) 2. При торможении электронов пучка возникают рентгеновские лучи. Напряжение между анодом и катодом достигает нескольких десятков киловольт. В трубке создаётся глубокий вакуум; давление газа в ней не превышает 10^-5 мм рт. ст.

Согласно проведённым исследованиям, рентгеновские лучи действовали на фотопластинку, вызывали ионизацию воздуха, не взаимодействовали с электрическими и магнитными полями. Сразу же возникло предположение, что рентгеновские лучи — это электромагнитные волны, которые в отличие от световых лучей видимого участка спектра и ультрафиолетовых лучей имеют гораздо меньшую длину волны. Но если рентгеновское излучение представляет собой электромагнитные волны, то оно должно обнаруживать дифракцию — явление, присущее всем видам волн. Дифракцию рентгеновских волн удалось наблюдать на кристаллах. Кристалл с его периодической структурой и есть то устройство, которое неизбежно должно вызвать заметную дифракцию рентгеновских волн, так как длина их близка к размерам атомов.