Вариант 8

Часть 1.

Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.

Прочитайте внимательно текст и выполните задания 1–5

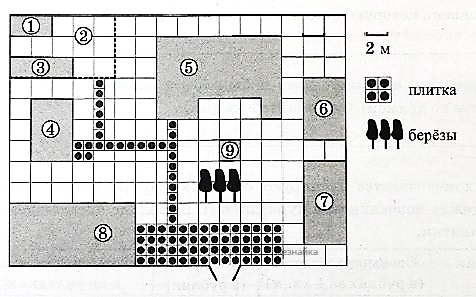
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма. Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.

Сопоставьте объекты, указанные в таблице, с цифрами, которыми эти объекты обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность из пяти цифр.

Объекты	баня	курятник	пруд	коровник	фонтан
Цифры

Тротуарная плитка продаётся в упаковках по 12 штук. Сколько упаковок понадобилось купить владельцам домохозяйства для того, чтобы выложить все дорожки и площадку между коровником и курятником?

Найдите площадь, которую суммарно занимают баня и коровник. Ответ дайте в квадратных метрах.

Найдите расстояние от бани до фонтана (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.

Владельцы домохозяйства планируют обновить всю тротуарную плитку (и дорожки, и площадку между коровником и курятником). В таблице представлены условия трёх поставщиков плитки. Рассчитайте стоимость планируемого обновления для каждого поставщика и выберете самый выгодный.

Поставщик	Стоимость плитки (в руб. за 1 кв.м.)	Доставка (в руб.)	Работы по демонтажу старой плитки и по укладке новой (в руб.)
1	270	1000	10000
2	275	2000	7000
3	285	3000	6000

Найдите значение выражения

$\frac{2,1\cdot3,8}{7,6\cdot0,7}$

На координатной прямой обозначены точки A и B. Какое из приведенных ниже утверждений относительно значений A и B неверно?

Вариант 8

1) $\vert A\vert>\vert B\vert$

2) $A+B<0$

3) $A^2<B^2$

4) $-B-A>0$

Найдите значение выражения $(\sqrt7-\sqrt3)^2$

1) 4

2) $10-\sqrt{21}$

3) $4-\sqrt{21}$

4) $10-2\sqrt{21}$

Найдите меньший корень уравнения

$\frac5{11-x}=\frac x6$

В упаковке находятся 500 воздушных шаров двух цветов. Определите, сколько среди них красных, если известно, что при случайном выборе вероятность достать из упаковки не красный шар равна 0,85.

Установите соответствие между графиком и верным для него утверждением.

A) 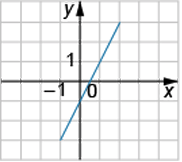Вариант 8

Б) 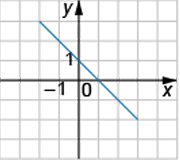В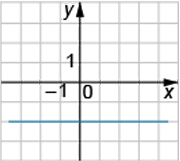ариант 8

В) Вариант 8

1) $y=2x-1$

2) $y=-2x+1$

3) $y=-x+1$

4) $y=-2$

Последовательность задана условиями: b₁ = —17, b_n+1 = 2 + b_n, $n\in Z$

Найдите количество отрицательных членов данной последовательности.

Упростите выражение $\frac1{ab}(\frac{a^2b}{a^2-b^2}-\frac{b^2a}{b^2-a^2})$ и найдите его значение при a = 114, b = 112.

Период колебаний пружинного маятника (в секундах) можно найти по формуле $T=2\pi\sqrt{\frac mk}$ , где m — масса груза, закрепленного на пружине (в кг), k — жесткость пружины (в Н/м). Определите массу закрепленного на пружине груза, если известно, что период колебаний составляет 8π секунд, а жесткость пружины равна 2 Н/м.

Установите соответствие между неравенством (обозначено буквами) и множеством его решений (обозначено цифрами).

А) $x^2<400$

Б) $x^2<-400$

В) $x^2>400$

Г) $x^2>-400$

1) $(-\infty;-20)\cup(20;+\infty0$

2) $(-\infty;+\infty)$

3) нет решений

4) $(-20;\;20)$

Сумма трёх углов равнобедренной трапеции равна $295^\circ$ . Чему равен бо́льший из углов данной трапеции? Ответ дайте в градусах.

Окружность, длина которой равна $14\pi\sqrt2$ см, описана около квадрата. Найдите периметр квадрата (в см).

Найдите площадь треугольника ABC (в см²), если известно, что сторона АС в полтора раза больше ВС, ВС = 12 см, а $\angle ABC+\angle BAC=150^\circ$

Найдите котангенс угла, изображённого на рисунке.

Вариант 8

Какие из приведённых ниже утверждений верны? Выберите 2 варианта из списка.

1) Один из углов треугольника всегда не превышает $60^\circ$

2) Длина окружности в два раза больше её радиуса.

3) В любом треугольнике центры вписанной и описанной окружностей совпадают.

4) Все точки плоскости, равноудаленные от заданной точки, лежат на одной окружности.

Часть 2.

При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.

Найдите наибольшее целое число, удовлетворяющее неравенству $x(1-\sqrt2)>3,8(1-\sqrt2)$

Показать ответ

x(1-√2)>3,8(1-√2)

Так как (1-√2)<0 , то

x<3,8 → наибольшее целое число 3

Ответ: 3

К раствору, содержащему 40г соли, добавили 200г воды, после чего концентрация уменьшилась на 10%. Сколько воды содержал раствор и какова была его концентрация?

Показать ответ

Пусть х г воды содержал раствор, тогда его концентрация составляла 40/(х+40). После того как добавили 200г воды, концентрация раствора составила 40/(х+40+200), что на 10%/100%=0,1 меньше первоначальной концентрации.

$\frac{40}{х+40}-\frac{40}{х+240}=0,1$

$40\left(х+240\right)-40\left(х+40\right)-0,1\left(х+240\right)\left(х+40\right)=0$

$40х+9600-40х-1600-0,1х^2-28х-960=0$

$х^2+280х-70400=0$

$D=280^2-4\cdot1\cdot(-70400)=360000$

$х_1=\frac{-280-\sqrt{360000}}2=-440$ - условию задачи не удовлетворяет

$х_2=\frac{-280+\sqrt{360000}}2=160$ грамм воды было первоначально в растворе

40/(40+160)=0,2 → 20% первоначальная концентрация раствора

Ответ: 160г, 20%

Постройте график функции 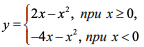Вариант 8 и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки

Показать ответ

1) Сначала построим у=2х-х², при х≥0

у=2х-х²=-х²+2х-1+1=-(х-1)²+1 - парабола, ветви вниз, вершина (1;1)

Вариант 8

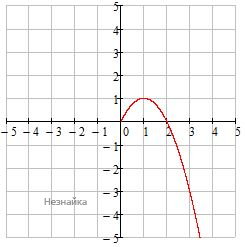
2) у=-4х-х², при х<0

у=-4х-х²=-х²-4х-4+4=-(х+2)²+4 - парабола, ветви вниз, вершина (-2;4)

Вариант 8

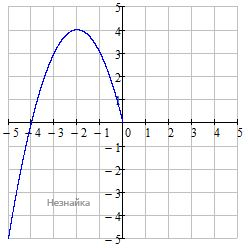
3) Совмещаем оба графика и находим m, при которых прямая y=m имеет с графиком ровно три общие точки.

Вариант 8

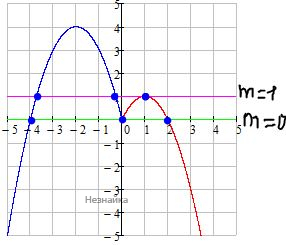
Ответ: 0;1

В треугольник АВС вписана окружность с центром в точке О. Луч АО пересекает сторону ВС в точке К. Найдите площадь треугольника АВС, если АВ=13, АС=15, ВК=6,5.

Показать ответ

Вариант 8

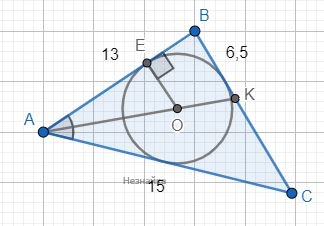
Центром окружности вписанной в треугольник, является точка пересечения биссектрис. Следовательно АК - биссектриса.

По свойству биссектрисы:

$\frac{CK}{BK}=\frac{AC}{AB}$

$CK=\frac{AC}{AB}\cdot BK=\frac{15}{13}\cdot6,5=7,5$

ВС=ВК+СК=6,5+7,5=14

По формуле Герона:

$p=\frac{AB+BC+AC}2=\frac{13+14+15}2=21$

$S=\sqrt{p(p-AC)(p-AB)(p-BC)}=\sqrt{21\cdot(21-13)(21-14)(21-15)}=$

$=\sqrt{21\cdot8\cdot7\cdot6}=\sqrt{7\cdot3\cdot2\cdot2\cdot2\cdot7\cdot2\cdot3}=7\cdot3\cdot2\cdot2=84$

Ответ: 84

Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках М и К соответственно. Докажите, что BМ = DК.

Показать ответ

Вариант 8

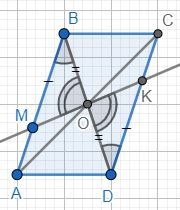
Диагонали параллелограмма делятся пополам в точке пересечения, следовательно △OBA=△ODC.

Тогда ∠OBA=∠ODC и OB=OD. ∠BOM=∠DOK - как вертикальные углы. Значит △BOM=△DOK по стороне и двум прилежащим углам.

Таким образом BМ=DК

В параллелограмме ABCD угол А равен 80°, сторона АВ равна 7. Биссектриса угла при вершине А пересекает сторону CD в точке Е. Найдите радиус окружности, касающейся отрезка АВ и лучей ВС и АЕ.

Показать ответ

Вариант 8

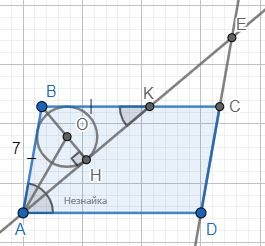
Биссектриса AE пересекает BC в точке K. Углы ∠BKA=∠DAE - как накрест лежащие, ∠BAK=∠DAE - AE биссектриса, следовательно, ∠BKA=∠BAK, значит △ABK равнобедренный. Тогда AB=BK=7 и ∠BKA=∠BAK=40°

Центр вписанной окружности - точка пересечения биссектрис. Проведем AO биссектрису ∠BAH и BH высоту △ABK → OH - радиус окружности.

Треугольник △ABH прямоугольный:

$cos\angle HAB=\frac{AH}{AB}\rightarrow AH=ABcos\angle HAB$

Треугольник △AOH прямоугольный

$tg\angle HAO=\frac{OH}{AH}$

$OH=AHtg\angle HAO=ABcos\angle HABtg\angle HAO=7cos40^\circ tg20^\circ$

Ответ: 7cos40° tg20°

0 из 0

№	Ваш ответ	Ответ и решение	Первичный балл
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения.