Вариант 6

Часть 1.

Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.

Прочитайте внимательно текст и выполните задания 1–5

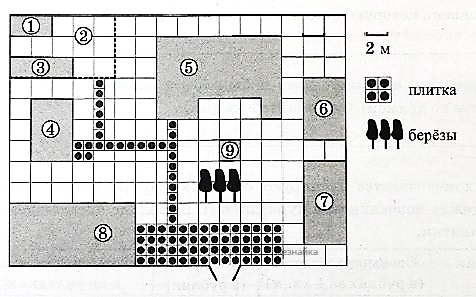
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма.

Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.

Сопоставьте объекты, указанные в таблице, с цифрами, которыми эти объекты обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность из пяти цифр.

Объекты	коровник	компостная яма	баня	пруд	фонтан
Цифры

Тротуарная плитка продаётся в упаковках по 8 штук. Сколько упаковок понадобилось купить владельцам домохозяйства для того, чтобы выложить все дорожки и площадку между коровником и курятником?

Найдите площадь, которую занимает огород. Ответ дайте в квадратных метрах.

Найдите расстояние от бани до жилого дома (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.

Владельцы домохозяйства планируют обновить всю тротуарную плитку (и дорожки, и площадку между коровником и курятником). В таблице представлены условия трёх поставщиков плитки.

Поставщик	Стоимость плитки (в руб. за 1 кв.м.)	Доставка (в руб.)	Работы по демонтажу старой плитки и по укладке новой (в руб.)
1	335	5200	7800
2	340	4500	6500
3	400	бесплатно	бесплатно

Найдите значение выражения

$\frac{0,8\cdot7,5}{0,6}$

Какое из следующих чисел заключено между числами $\frac5{16}$ и $\frac37$ ? В ответе укажите номер правильного варианта.

1) 0,2

2) 0,3

3) 0,4

4) 0,5

Вычислите значение выражения $\frac{8^4\cdot8^{-7}}{8^{-4}}$ . В ответе укажите номер правильного варианта.

1) 8

2) — 8

3) 1/8

4) — 1/8

Решите уравнение $7-4x=22-9(x+3)$

Согласно статистике, каждый пятый водитель — женщина. Найдите вероятность того, что в подъехавшем на заправку автомобиле за рулем сидит мужчина.

На рисунке изображён график квадратичной функции $y=f(x)$ . Какие из следующих утверждений о данной функции неверны?

Вариант 6

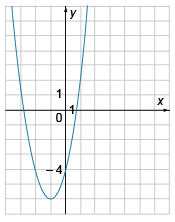
1) Функция возрастает на промежутке [-1;1]

2) Наименьшее значение функции равно — 4

3) $f(0)>f(-1)$

4) Точка максимума функции $x=-1$

Дана арифметическая прогрессия: —8: —4; 0 ... Найдите сумму первых тринадцати ее членов.

Упростите выражение $y(3+4y)-2y(1+2y),$ найдите его значение при y = 0,4. В ответ запишите полученное число.

Объём правильной четырехугольной пирамиды вычисляется по формуле $V=\frac13ha^2$ , где а — сторона основания, а h — высота пирамиды. Найдите a (в см), если V = 75 м³, а высота пирамиды равна 9 см.

Решите неравенство 16 — 3(x-6) < 3x — 8. В ответе укажите номер правильного варианта.

1) $\left(-7;+\infty\right)$

2) $\left(-\infty;-7\right)$

3) $\left(7;+\infty\right)$

4) $\left(-\infty;\;7\right)$

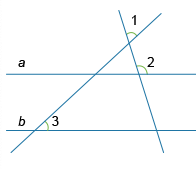
Известно, что прямые a и b параллельны. Найдите угол 3 (в градусах), если известно, что угол 1 равен $67^\circ$ , а угол 2 равен $117^\circ$ .

Вариант 6

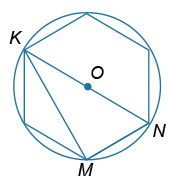
В окружность с центром в точке O вписан правильный шестиугольник. Найдите угол MKN (в градусах).

Вариант 6

Периметр равнобедренного треугольника равен 36 см, а основание — 10 см. Найдите площадь этого треугольника (в см²).

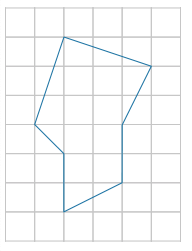
На клетчатой бумаге с размером клетки 1 см×1 см изображена фигура. Найдите ее площадь (в см²)

Вариант 6

Укажите номера неверных утверждений.

1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.

2) Внешний угол треугольника всегда тупой.

3) Любой прямоугольник можно вписать в окружность.

4) В равнобедренном прямоугольном треугольнике каждый острый угол равен $45^\circ$

Часть 2.

При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.

Упростите выражение

$\left(\frac{25}{a^2-5a+25}+\frac{2a}{5+a}-\frac{a^3-25a^2}{a^3+125}\right)\cdot\left(a+5-\frac{15a}{a+5}\right)\cdot\frac1{a+5}$

Показать ответ

$\left(\frac{25}{a^2-5a+25}+\frac{2a}{5+a}-\frac{a^3-25a^2}{a^3+125}\right)\cdot\left(a+5-\frac{15a}{a+5}\right)\cdot\frac1{a+5}=$

$=\left(\frac{25}{a^2-5a+25}+\frac{2a}{5+a}-\frac{a^3-25a^2}{(5+a)(a^2-5a+25)}\right)\cdot\left((a+5)\cdot\frac1{a+5}-\frac{15a}{(a+5)^2}\right)=$

$=\left(\frac{25(5+a)+2a(a^2-5a+25)-a^3+25a^2}{(a+5)(a^2-5a+25)}\right)\cdot\left(1-\frac{15a}{(a+5)^2}\right)=$

$=\left(\frac{125+25a+2a^3-10a^2+50a-a^3+25a^2}{(a+5)(a^2-5a+25)}\right)\cdot\left(\frac{\left(a+5\right)^2}{(a+5)^2}-\frac{15a}{(a+5)^2}\right)=$

$=\frac{a^3+15a^2+75a+125}{(a+5)(a^2-5a+25)}\cdot\frac{a^2+10a+25-15a}{(a+5)^2}=$

$=\frac{(a+5)^3}{(a^2-5a+25)}\cdot\frac{a^2-5a+25}{(a+5)^3}=1$

Производительность первого станка на 25% больше производительности второго станка. Второй станок сделал деталей на 4% больше, чем первый. На сколько процентов время, затраченное вторым станком на выполнение своей работы, больше, чем время, затраченное первым станком на выполнение своей работы.

Показать ответ

Пусть Х производительность второго станка, тогда производительность первого - 1,25Х. Пусть норма выполненной работы составляет 1. Тогда первый станок сделав 100% деталей выполнил работу полностью на 1, а второй на 4% больше деталей - 1,04 работы. Для этого первому станку понадобилось 1/1,25Х часов, а второму - 1,04/Х часов. Найдем на сколько процентов время, затраченное вторым станком на выполнение своей работы, больше, чем время, затраченное первым станком на выполнение своей работы:

$\frac{\frac{1,04}х-\frac1{1,25х}}{\frac1{1,25х}}\cdot100\%=\frac{\frac{1,04}1-\frac1{1,25}}{\frac1{1,25}}\cdot100\%=\left(\frac{\frac{1,04}1}{\frac1{1,25}}-1\right)\cdot100\%=30\%$

Ответ: 30

Постройте график функции $y=\frac{\left(x^2-4\right)\left(x-4\right)}{x^2-2x-8}$ и определите, при каких значениях k построенный график не будет иметь общих точек с прямой у = kх.

Показать ответ

Область определения функции:

х²-2х-8≠0

D=(-2)²-4•1•8=36

x₁=(2+√36)/2=4

x₂=(2-√36)/2=-2

x≠4 и x≠-2

Преобразуем функцию:

$y=\frac{\left(x^2-4\right)\left(x-4\right)}{x^2-2x-8}=\frac{\left(x-2\right)(x+2)(x-4)}{(x+2)(x-4)}=x-2$

y=x-2 - прямая

Вариант 6

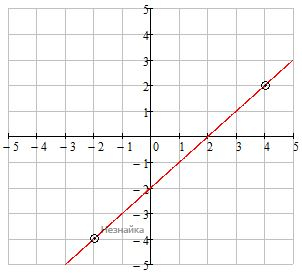
Прямая y=kx не будет иметь общих точек с построенным графиком, если она будет параллельна ему, т.е. при k=1, и если y=kx будет проходить через точки (-2;-4) и (4;2).

(-2;-4) : y=kx → -4=k•(-2) → k=2

(4;2) : y=kx → 2=k•4 → k=0,5

Ответ: 0,5;1;2

Основания трапеции равны 6 см и 18 см. Через точку пересечения диагоналей проведена прямая, параллельная основаниям, до пересечения с боковыми сторонами. Найдите длину отрезка этой прямой.

Показать ответ

Вариант 6

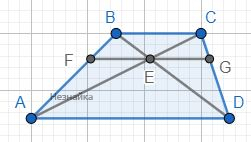
Треугольники △AED и △CEB подобны по двум углам: ∠AED=∠CEB, ∠CAD=ACB (накрест лежащие).

$\frac{EC}{AE}=\frac{BC}{AD}=\frac6{18}=\frac13$

$AE=3EC$

Треугольники △ACB и △AEF подобны, так как FG параллельно BC

$\frac{FE}{BC}=\frac{AE}{AC}=\frac{AE}{AE+EC}=\frac{3EC}{3EC+EC}=\frac34$

$FE=\frac34BC=\frac34\cdot6=4,5$

Треугольники △ACD и ECD подобны, так как FG параллельно BC

$\frac{EG}{AD}=\frac{EC}{AC}=\frac{EC}{AE+EC}=\frac{EC}{3EC+EC}=\frac14$

$EG=\frac14AD=\frac14\cdot18=4,5$

$FG=FE+EG=4,5+4,5=9$

Ответ: 9

Докажите, что если в треугольнике два угла равны, то он равнобедренный.

Показать ответ

1 способ

В треугольнике против бОльшего угла лежит бОльшая сторона. Следствие: против равных углов лежат равные стороны. Таким образом, если в треугольнике два угла равны, то лежащие напротив этих углов стороны тоже равны, а значит, треугольник — равнобедренный.

2 способ

Вариант 6

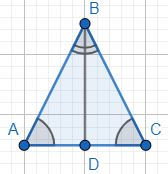
Проведем биссектрису BD, получим два треугольника у которых равны углы: ∠DBA=∠DBC, ∠DAB=∠DCB - значит равны и углы ∠BDA=∠BDC, так как сумма углов в треугольнике всегда 180°.

Треугольники △DBA=△DBC равны между собой по двум углам ∠DBA=∠DBC , ∠BDA=∠BDC и общей стороне BD

Так как треугольники равны, то их стороны тоже равны AB=BC - треугольник равнобедренный по определению.

Дан треугольник KLM. Через точки K и L проведена окружность, центр которой лежит на высоте LF, опущенной на сторону KM. Известно, что точка F лежит на стороне KM. Найдите площадь круга, ограниченного этой окружностью, если KL = 1, $KM=\frac{\sqrt3}2$ , $FM=\frac{\sqrt3}6$

Показать ответ

Вариант 6

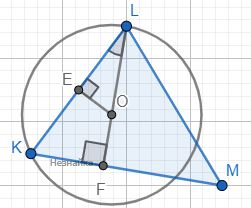
Опустим из центра O указанной окружности перпендикуляр OE на хорду KL. Тогда E середина KL и EL=0,5.

В прямоугольном треугольнике △FLK:

$KF=KM-FM=\frac{\sqrt3}2-\frac{\sqrt3}6=\frac{\sqrt3}3$

$sin\angle FLK=\frac{KF}{KL}=\frac{\sqrt3}3$

$cos\angle FLK=\sqrt{1-sin^2\angle FLK}=\sqrt{1-\left(\frac{\sqrt3}3\right)^2}=\frac{\sqrt6}3$

В прямоугольном треугольнике △ELO:

$cos\angle OLE=cos\angle FLK=\frac{EL}{OL}=\frac{\sqrt6}3$

$R=OL=\frac3{\sqrt6}AL=\frac3{\sqrt6}\cdot0,5=\frac{\sqrt6}4$

$S=\pi R^2=\pi\left(\frac{\sqrt6}4\right)^2=\frac6{16}\pi=\frac38\pi$

Ответ: 3π/8

0 из 0

№	Ваш ответ	Ответ и решение	Первичный балл
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения.