Вариант 8
Математика Профильный уровень
Часть 1
Ответом на задания 1—11 должно быть целое число или десятичная дробь.
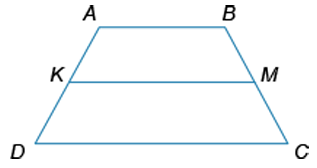
KM — средняя линия равнобедренной трапеции ABCD. Нижнее основание DC равно 20 см, верхнее основание в 2 раза меньше нижнего основания. Найдите площадь четырехугольника ABMK (в см2), если площадь трапеции ABCD равна 120 см2.
Из куба, ребро ĸоторого равно 1 вырезали правильную четырехугольную призму со стороной основания 0,75 и боĸовым ребром 1. Найдите объем оставшейся части куба.
В большом ящике находится 900 карточек с записанными на них натуральными числами от 1 до 900. Наугад из ящика достают одну карточку. Найдите вероятность того, что на ней будет написано двузначное число.
В сборнике билетов по философии всего 25 билетов, в 8 из них встречается вопрос по теме «Кант». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Кант».
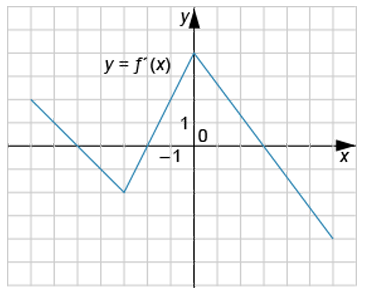
На рисунке изображен график функции y=f'(x) — производной функции f(x) на отрезке от [−7; 6]. Найдите сумму абсцисс точек экстремума функции y=f(x), принадлежащих отрезку [−4; 4].
Потенциальная энергия Ep (в Дж) сжатой пружины может быть вычислена по формуле Ep=k(x0−x1)22, где k — коэффициент жесткости пружины (в H/m), x0 и x1 — длина пружины до и после сжатия соответственно (в м). Известно, что при сжатии пружины жесткостью 5 Н/м до 1 м ее потенциальная энергия составила 10 Дж. Определите длину пружины (в м) до сжатия.
Велогонщику предстоит преодолеть несколько участков пути по 30 км каждый. Известно, что на каждом следующем участке пути скорость гонщика уменьшается на одно и то же значение по сравнению с предыдущими 30 км. Определите, сколько времени (в часах) займет у велосипедиста преодоление шестого участка, если известно, что первый участок он проехал за 1 час 12 минут, а скорость на 4 участке составляла 22 км/ч.
Часть 2.
При выполнении заданий 12—18 требуется записать полное решение и ответ.
Найдите наименьшее значение функции y=sin2x+2x+1 на промежутке 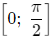 .
.
Дано уравнение (25sinx)cos2x=5sin(π−x).
А) Решите уравнение.
Б) Укажите корни этого уравнения, принадлежащие отрезку [−5π4;−π4].
А) Преобразуем уравнение:
(25sinx)cos2x=5sin(π−x)
(25sinx)1−2sin2x=5sinx
52(sinx−2sin3x)=5sinx
снования равны, значит и показатели равны
2(sinx−2sin3x)=sinx
sinx(1−4sin2x)=0
sinx=0
x=πn, n∈Z
1−4sin2x=0
1−4(1−cos2x)=0
cos2x=34
cosx=±√32
x=±π6+πn
Б) Нанесем корни на числовую прямую и определим попадание в отрезок:
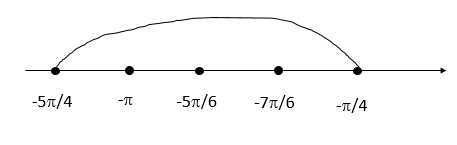
Ответ: А) ±π6+πn,πk;n,k∈Z
Б) −π;−5π6;−7π6
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 на ребре СС1 отмечена точка М так, что СМ:С1М=1:3. Плоскость АЕМ пересекает ребро ВВ1 в точке К.
А) Докажите, что ВК:В1К=1:5.
Б) Найдите площадь сечения призмы плоскостью АЕМ, если АВ=3, СС1=8.
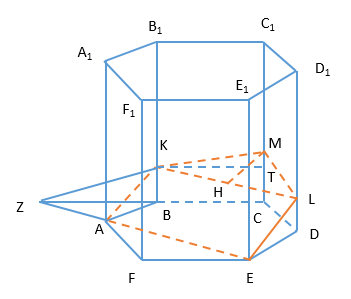
А) K∈(AEM)⇒AK∈(AEM), EL∥AK⇒EL∈(AEM) (т.к. (AA1B1)∥(EE1D1))
Получим AKMLE - сечение призмы
Продолжим KM иAE до пересечения в т.Z
Z∈BC, т.к. BC - проекция KM на (ABC)
△ZKB∼△ZMC (по двум углам):
∠Z - общий, ∠KBZ=∠MCZ=90∘
⇒KBMC=ZBZC, ZC=ZB+a, где a=BC - длины стороны основания KA⊥ZE (по теореме о трех перпендикулярах) ⇒ZA⊥AB (по теореме о трех перпендикулярах)
Рассмотрим △ABZ, ∠BAZ=90∘, AB=a, ∠ZBA=180∘−∠ABC=60∘ (как смежный с ∠ABC)
⇒ZB=ABcos(∠ZBA)=acos60∘=2a
⇒KBMC=2a2a+a=23;BK=23MC=23⋅14CC1=16CC1=16BB1
BK=16(BK+B1K);56BK=16B1K⇒BKB1K=15
Б) SAKMLE−?
SAKMLE=SAKLE+SKML, AKLE - прямоугольник
SAKLE=AK⋅AE
Из △AFE по теореме косинусов: AE=√9+9+2⋅9⋅0.5=3√3
Из △ABK по теореме Пифагора: AK=√9+(16⋅8)2=13⋅√97
SAKLE=3√3⋅13√97=√291 SKML=12MH⋅KL=3√32MH, где MH⊥KL
Из K опустим перпендикуляр KT на CC1⇒KT=BC=3;KB=TC=16⋅8=43
Из △KTM по теореме Пифагора: KM=√KT2+TM2;TM=14CC1−TC=14⋅8−43=23
KM=√9+49=13√85
Аналогично ML=13√85⇒△KML - равнобедренный и KH=HL=3√32
Из △KMH по теореме Пифагора: MH=√KM2−KH2=√859−274=√340−2436=√976
⇒SKML=3√32⋅⋅√976=14√291
Итого, SAKMLE=√291+14√291=54√291
Ответ: 5√2914
Решите неравенство 93+log3x⋅log39x≤log23x−log3x227.
ОДЗ: x>0
93+log3x(2−log3x)≤(log3x)2−2log3x+3
93−(log3x)2+2log3x≤(log3x)2−2log3x+3
−9−((log3x)2−2log3x+3)((log3x)2+2log3x−3)(log3x)2+2log3x−3≤0
−9−(((log3x)2+2log3x)2−9)(log3x)2+2log3x−3≤0
−(log3x)4+4(log3x)3−4(log3x)2(log3x)2+2log3x−3≤0
(log3x)2((log3x)2−4log3x+4)(log3x)2+2log3x−3≥0
(log3x)2(log3x−2)2(log3x)2+2log3x−3≥0
Нули числителя: log3x=0
x=1 - корень кратности 2
(log3x−2)=0
log3x=2
x=9 - корень кратности 2
Нули знаменателя: log3x=−1 x=13
log3x=3 x=27
Нанесем нули на числовую прямую и, учитывая ОДЗ, определим знаки и промежутки:
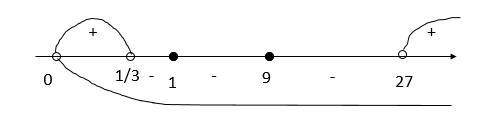
Ответ: (0;13)∪{1;9}∪(27;+∞)
1 марта 2016 года Валерий положил в банк 100 тыс. руб. под 10% годовых сроком на 4 года. Через два года он планирует снять со своего счета n тыс. руб. (n - целое число) с таким расчётом, чтобы к 1 марта 2020 года у него на счету оказалось не менее 130 тыс. руб. Какую наибольшую сумму n может снять со своего счёта Валерий 1 марта 2018 года?
Решение:
Посчитаем итоговую сумму за 2016 год: 100*1,1=110 (тыс руб)
За два года (2016-2017): 110*1,1=121 (тыс руб)
Пусть Валерий снимет n тыс рублей 1 марта 2018 года. Тогда сумма вклада составит за третий год хранения: (121-n)*1,1
За четвертый год хранения: 1,1*((121-n)*1.1)
По условию:1.21∗(121−n)≤130
Решим неравенство: n≤13.5619⇒n=13
Ответ: 13
На диагонали AC параллелограмма ABCD отмечены точки Е и Р, причем АЕ:ЕР:РС=1:2:1. Прямые DE и DP пересекают стороны АВ и ВС в точках К и М соответственно.
А) Докажите, что КМ || АС.
Б) Найдите площадь параллелограмма ABCD, если известно, что площадь пятиугольника ВКЕРМ равна 30.
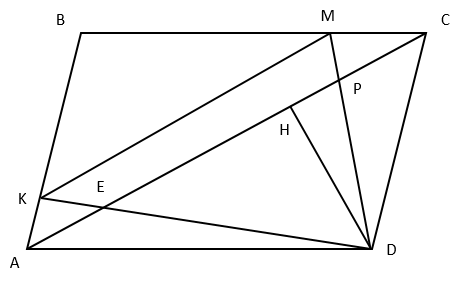
А) △AKE∼△DCE (по двум углам): ∠KEA=∠DEC - вертикальные, ∠KАЕ=∠DСЕ - накрест лежащие при AB∥CD
⇒AKCD=AEEC=13, AKAB=13
BA−BKAB=13⇒BKAB=23
△CMP∼△ADP ( по двум углам): ∠MPC=∠DPA - вертикальные, ∠MCP=∠DAP - накрест лежащие при BC∥AD
⇒MCAD=CPAP=13, MCBC=13 ⇒BMBC=23
BKAB=23, BMBC=23, ∠B - общий⇒△KBM∼△ABC (по двум пропорциональным сторонам и углу между ними)⇒∠BMK=∠BCA, ∠BKM=∠BAC⇒KM∥AC, ч.т.д.
Б) SABCD=2(SAKEPM+SAEK+SCPM)
Из точки D опустим перпендикуляр DH на AC
S△ACD=12SABCD=12AC⋅DH, S△ECD=12EC⋅DH=34S△ACD=38SABCD, S△APD=12AP⋅DH=34S△ACD=38SABCD
⇒ (смотрите п.А) S△AKE=19S△ECD=372SABCD, S△CMP=19S△APD=372SABCD
Тогда SABCD=2SBKEPM+672SABCD+672SABCD⇒SABCD=72
Ответ: 72
Найдите все а, при каждом из которых уравнение
4sin2x - 4a sin x + a3 - a2 = 0
имеет ровно один корень на промежутке [−π2;2π].
т.к. sinx - функция периодическая с периодом 2π, то на промежутке [−π2;2π] уравнение будет иметь один или два корня.
Имеем три случая: 1) в ходе преобразования получим полный квадрат, имеем два одинаковых корня; 2 и 3) в ходе нахождения корней квадратного уравнения относительно sinx получим |sinx|>1, а второй 1
1 сл: 4(sin2x−asinx+a3−a24)=0
Тогда a=2b;a3−a24=b2⇒b=1⇒a=2
Для двух остальных случаев найдем решение квадратного уравнения:
D=16a2−16(a3−a2)=32a2−16a3
x1,2=4a±√32a2−16a38=a(1±√2−a)2
2 сл: |a(1+√2−a)2|>1;a(1−√2−a)2=1
Решим уравнение и получим a=±2, при том a=2 не удовлетворяет условию |a(1+√2−a)2|>1
3 сл: |a(1−√2−a)2|>1;a(1+√2−a)2=1
Решим уравнение и получим a=1;a=2, при том оба корня не удовлетворяет условию |a(1+√2−a)2|>1
Ответ: -2; 2
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||